Introdução ao modo ativo/ dinâmico do Processing (finalmente!).
Nesta sessão/aula aborda-se:
- Modo Ativo / Dinâmico (tweak & debug modes);
- Funções e Parâmetros (declaração e invocação de funções personalizadas)
- Transformações (pushMatrix)
- Vetores (arrays) uni-dimensionais
O modo ativo é a forma “natural” em que o Processing quer “correr”. Isto é, o Processing foi feito para criar gráficos interativos. E, para reagir ao utilizador, ou para fazer animações, é necessário trabalhar continuamente no “tempo”.
[See processing.org tutorials]
Isto introduz-nos às funções (automáticas) do Processing. Em primeiro lugar, o setup() — corre uma única vez, no arranque do programa e “serve” para configurar a aplicação e inicializar coisas como as variáveis.
E o draw() — corre “sempre que pode” —, que serve para desenhar e atualizar os gráficos e interação do utilizador com o computador / no ecrã. Corre a uma velocidade predefinida [confirmar defaults: 30–60 fps?]. E tenta manter uma velocidade constante. esta velocidade é definida pelo conceito de frames por segundo (frames per second FPS) [speed = frameRate]
O primeiro ponto a estudar no reference é a secção de Structure. Nomeadamente: o
// Inicializar programa void setup() { size(500, 500); } // Desenhar continuamente void draw() { background(255); }
No futuro, também podem tirar partido de uma função especial (que antecede o setup) e outros eventos e funções especiais do sistema
Mas esta fica para outro dia.
Este é o início do uso do modo dinâmico/ativo. Vamos continuar a usar o Processing da mesma forma. [UPDATE 2021: na realidade esta aula e o modo Processing/Java vai ficar por aqui… Este é o ano em que vamos dar o salto para p5.js a partir daqui insert fork URL]
Usando os mesmos blocos lógicos de organização do programa:
- Importar Bibliotecas;
- Declarar
- Objetos,
- Variáveis;
- Inicializar
- programa,
- objetos e
- variáveis, e;
- Desenhar (na realidade dentro do “bloco” de desenho ainda vamos ter outros dois blocos lógicos de:
- update e
- display… (mas isto fica para maiores detalhes no módulo 301).
Assim um programa simples em modo ativo, passa a ser feito da seguinte forma:
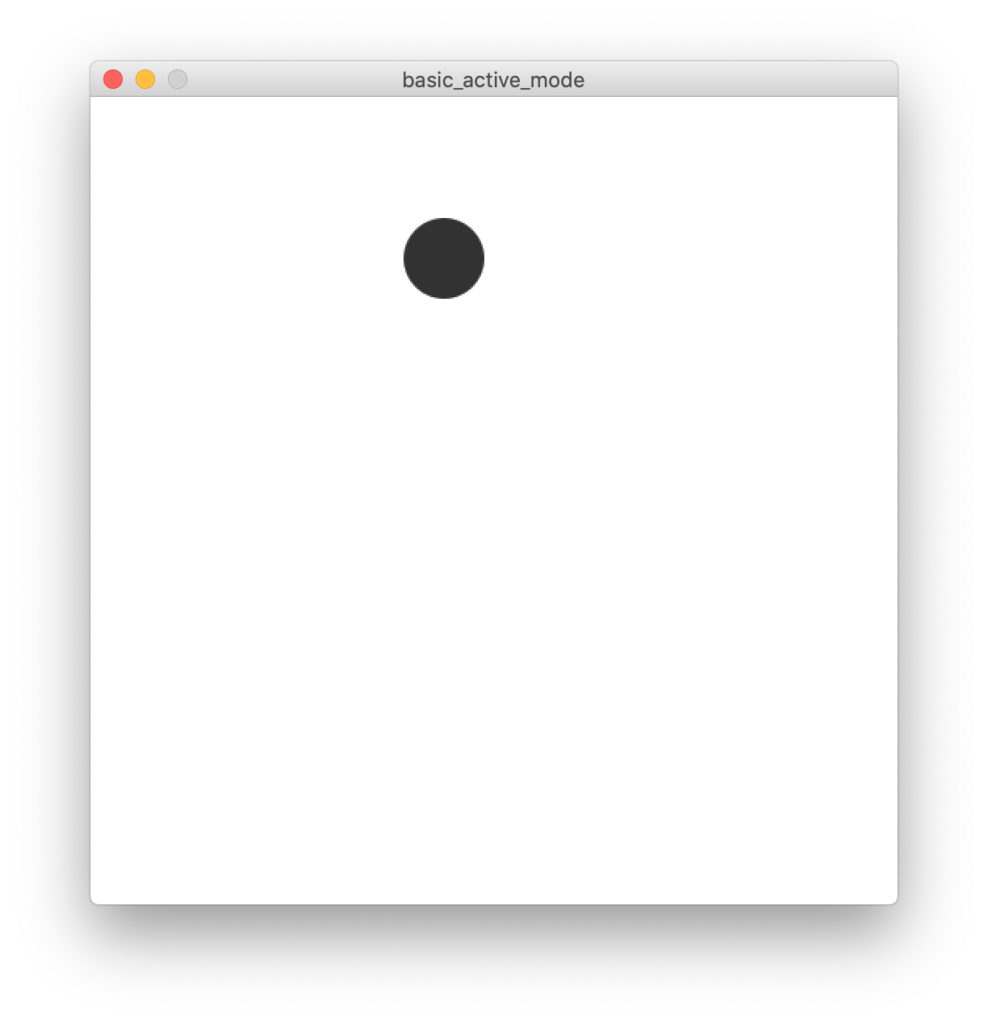
// importar bibliotecas import processing.pdf.*; // declarar objetos e variáveis int ballSize; // inicializar programa e variáveis void setup() { size(500, 500); background(255); frameRate(99); // set the refresh rate ballSize = 50; } // desenhar continuamente/repetidamente void draw() { // update calculation & graphics on screen background(255); noStroke(); fill(50); // display the new graphics / frame circle(mouseX, 100, ballSize); }
[ver ainda palavras reservadas / variáveis do sistema]
Tweak Mode
O TweakMode é um modo dinâmico que permite ajustar tudo o que são valores “hard-coded” nas primitivas gráficas (por exemplo) em tempo real. Isto dá jeito para quando estamos a experimentar alguns desenhos ou visualizações, e queremos afinar coordenadas ou valores enquanto o programa corre.
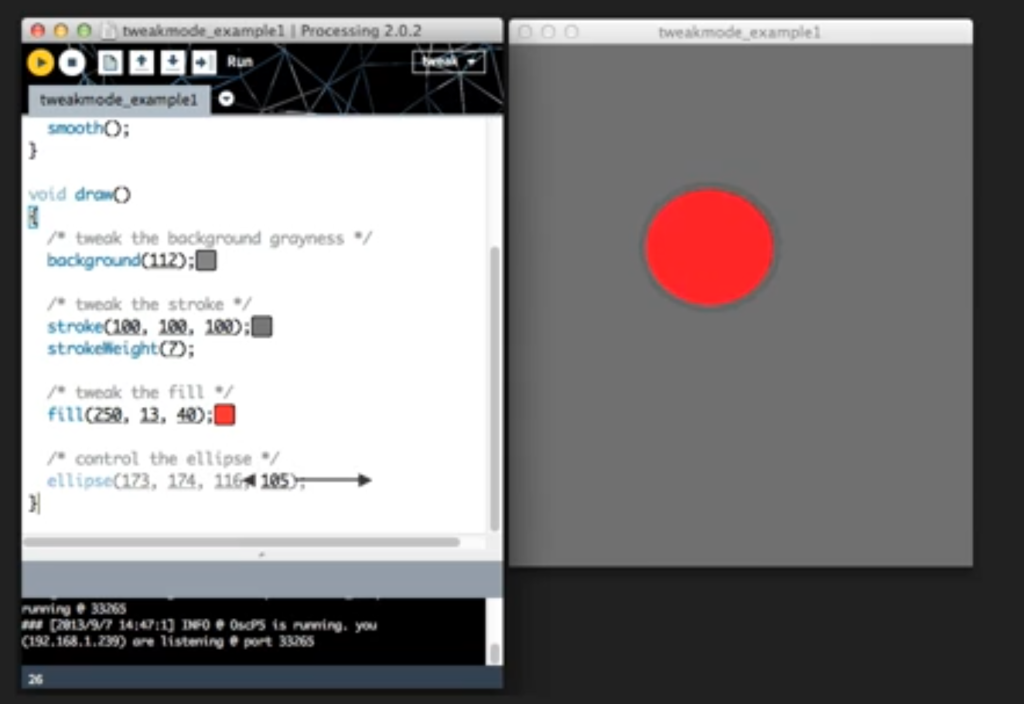
Para isso, basta fazer play e clicar e arrastar os valores (constantes / hardcoded) na janela de código do IDE.
Quando se para o programa, o Processing pergunta se queremos guardar os valores manipulados.
O Tweak e o Debug não têm propriamente uma explicação no reference… mas podemos sempre ver os vídeos do Shiffman para perceber melhor (ou os vídeos das aulas?)
Debug Mode
O modo de depuração do Processing não é um modo muito utilizado (talvez porque ainda não esteja muito desenvolvido?). Mas já é útil quando queremos interromper a execução e “ver” que variáveis e valores estão a ser calculadas.
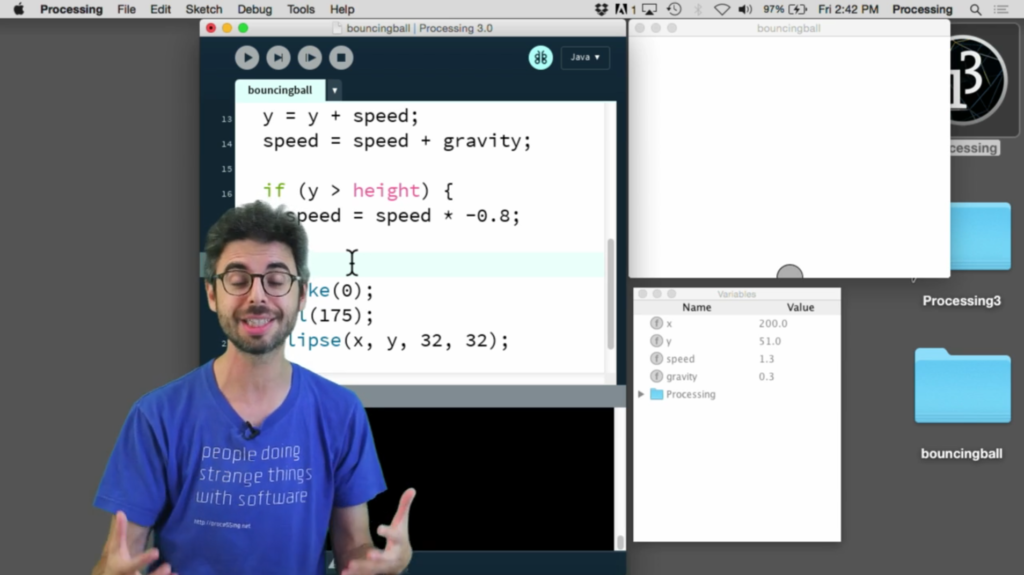
Esta ferramenta, apesar de poderosa, é recente e tal como o Shiffman nos diz, pode ser muito útil para “mergulhar” no código e variáveis. No entanto, fazer uma pausa para descansar, ou usar o println() para o Processing nos devolver os valores que queremos em tempo real é a minha estratégia preferida.
Os modos Tweak e Debug estão descritos aqui: https://processing.org/reference/environment/
Voltando ao modo ativo / dinâmico, depois de perceber o que acontece “em tempo”, convém conhecer mais opções do environment. Para quem está mais familiarizado, podem e devem pesquisar o seguinte.
Depois há coisas fixes (nem acredito que nunca fiz isto nas aulas!) como mudar o título e animar a posição da própria janela no ecrã do computador. Com um bocadinho de imaginação e focused até podemos fazer um mini-jogo irritante de “whack-a-mole” versão janela do computador?
Estas funções permitem controlar / manipular o fluxo normal do modo ativo/dinâmico. Isto é, permitem parar de “redesenhar”, ou pedir para interromper o fluxo normal e atualizar a meio do ciclo de draw() [mas o ideal é experimentar estas funções no final da aula / módulo após aprender a utilizar os eventos].
[considerar explicar o seguinte até ao final do semestre/ ou no futuro / ou para os programadores mais experientes]
Funções & Parâmetros
Funções (personalizadas) e parâmetros
Aquilo que vimos acima, com o “void setup()” e o “void draw()” acabam por organizar o nosso código em “blocos”. Isto é, agrupamos conjuntos de instruções em “grupos” lógicos” para modularizar / arrumar o código e tornar a execução mais eficiente.
Assim, as funções são uma espécie de “grupo” modular de código reutilizável. Não há uma secção específica para isto no reference (devia!). Mas compreende-se rapidamente vendo o Structure. Há dois tipos de funções:
(em Javascript ou em p5.js, aquilo que denominamos aqui por “void” vai-se chamar de “function”)
As funções setup e draw são funções especiais que são chamadas automaticamente pelo computador. Isto é, apenas as precisamos de declarar / escrever no programa que elas são executadas — Ah… e lembrem-se, o setup é chamado e executado apenas uma única vez, e o draw é chamado automaticamente à velocidade máxima (fps) possível, ou que estiver definida pelo frameRate().
Mas, tal como fizemos com os robôs (normalmente explico isto com a cabeça de lego), às vezes queremos desenhar o mesmo bloco de instruções mais do que uma vez.
E, tal como tenho vindo sempre a dizer, tudo o que se repete, ou melhor… sempre que repetimos instruções é sinal que podemos converter em variáveis, em ciclos ou automatizar / modularizar de alguma forma. é aqui que entram as funções personalizadas.
Até agora, temos estado sempre a usar funções. Mas são funções de sistema. Funções que o Processing já conhece. Por exemplo noFill(). Esta é uma função que diz ao Processing para desligar a cor de preenchimento.
Ou a função ellipse(10, 10, 30, 30) que diz ao Processing para desenhar um gráfico (círculo) redondo. Esta função inclui (envia) um conjunto de parâmetros (informações) que dizem ao Processing “onde” desenhar (no x = 10 e no y = 10) e com um tamanho específico (w = 30 e h = 30).
Esta é uma boa altura para falar da palavra “void” (que equivale a function) e das funções personalizadas.
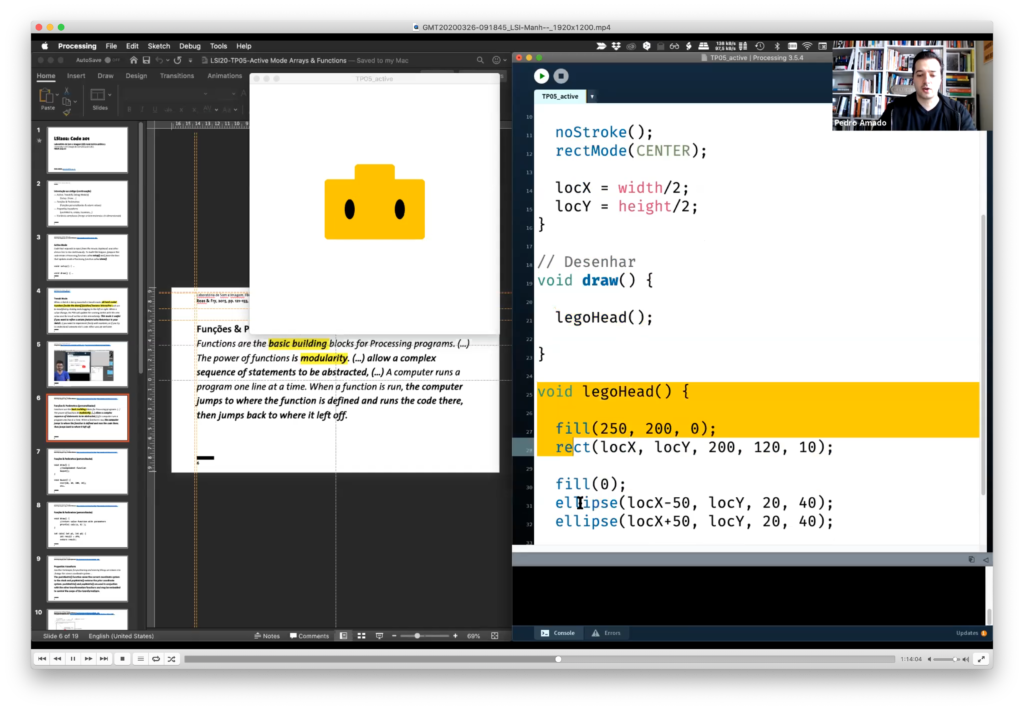
Quando queremos correr (desenhar?) um conjunto de gráficos específicos (personalizados), como p. ex. a nossa cabeça de lego, podemos “agrupar” todas as instruções num único bloco de código — numa função.
Para compreendermos as funções precisamos de entender o conceito de declaração e de invocação de funções.
// Desenhar void draw() { background(255); legoHead(); // invoca / chama a função }
Quando desenhamos uma ellipse, ou quando pedimos ao Processing para “limpar” o fundo do ecrã, os programadores do Processing já “ensinaram” ao Processing como o fazer. Para isso, invocamos a função “background();” e o Processing faz o resto.
Por isso, para “chamar” uma função, escrevemos o nome da função que queremos, seguida de “();“. A isto, a esta instrução específica, chama-se invocar uma função.
Mas, quando queremos desenhar uma cabeça de lego, o Processing não sabe o que fazer.
Então, precisamos de “ensinar” ao Processing um conjunto de instruções. A isto chamamos declarar uma função (personalizada). Assim, sempre que invocarmos, ou melhor, sempre que pedirmos, ou que chamarmos a função de cabeça de lego no ciclo do draw, o Processing “salta” para o bloco de código em que se descrevem as instruções para desenhar.
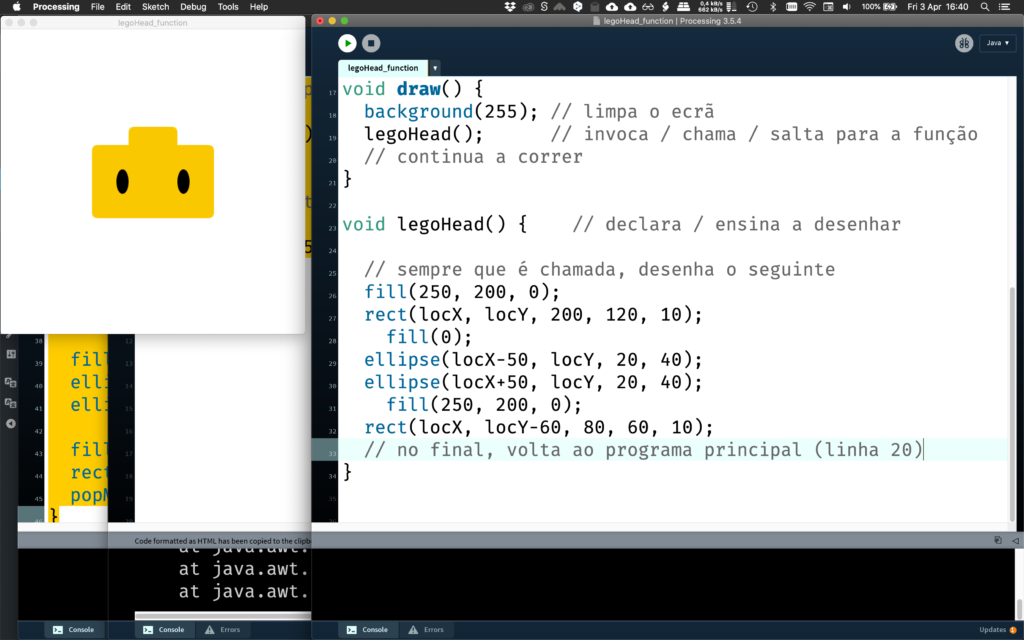
void draw() { background(255); // limpa o ecrã legoHead(); // invoca / chama a função // continua a correr }
Declaramos (descrevemos) o que / como fazer quando o utilizador quer uma função (p. ex. cabeça de lego) com void seguido de nome_da_função() { . Incluímos todas as instruções e cálculos dentro das chavetas para “agrupar” as instruções e executa-las todas juntas. E terminamos a função com a última chaveta }
void legoHead() { // declara / ensina a desenhar fill(250, 200, 0); rect(locX, locY, 200, 120, 10); fill(0); ellipse(locX-50, locY, 20, 40); ellipse(locX+50, locY, 20, 40); fill(250, 200, 0); rect(locX, locY-60, 80, 60, 10); }
A palavra void utiliza-se pois este bloco de código / conjunto de instruções corre/é executado quando é chamado e “não devolve” resultados. Corre e pronto. Volta ao sítio onde foi chamada e continua o programa principal.
Podemos desenhar outras funções que devolvem resultados. Por exemplo para calcular somas ou médias. Quando o fazemos, ao declarar a função temos que indicar o tipo de valor que vai ser devolvido ao programa principal. Indicar os parâmetros que são passados à função (mais à frente). E não esquecer que o resultado deve ser devolvido (e armazenado ou computado) no ciclo programa principal.
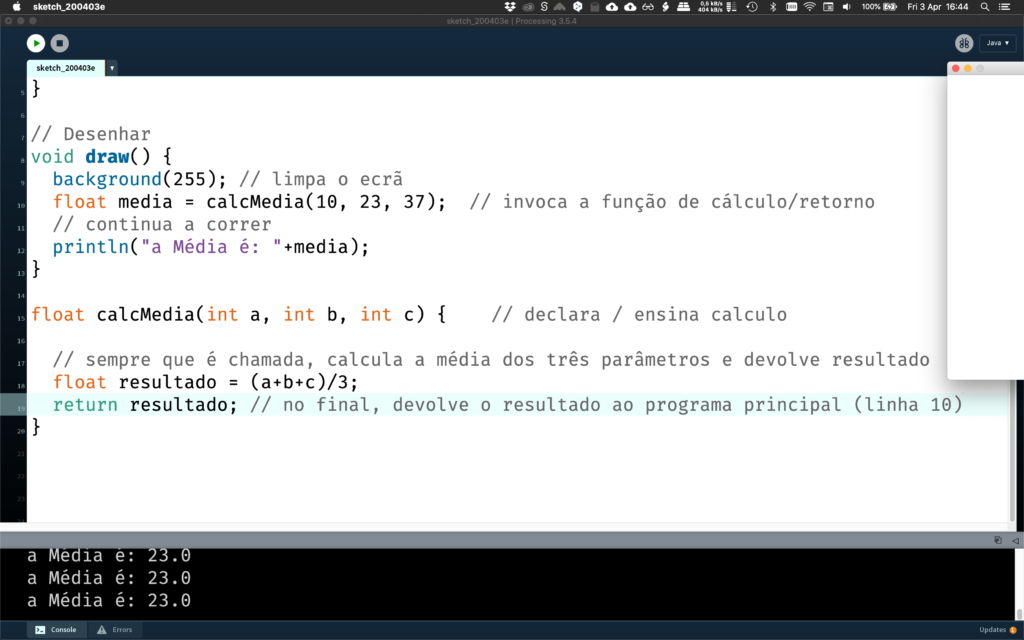
// Inicializar void setup() { size(500, 500); background(255); } // Desenhar void draw() { background(255); // limpa o ecrã float media = calcMedia(10, 23, 37); // invoca a função de cálculo/retorno // continua a correr println("a Média é: "+media); } float calcMedia(int a, int b, int c) { // declara / ensina calculo // sempre que é chamada, calcula a média dos três parâmetros e devolve resultado float resultado = (a+b+c)/3; return resultado; // no final, devolve o resultado ao programa principal (linha 10) }
Este tipo de função é mais específica. Mas já as temos utilizado. por exemplo, o random() é uma função deste tipo. “Devolve” um valor para usarmos.
Esta é uma boa altura para falar de parâmetros. Tal como a função random(), ou a função ellipse() pode levar um ou mais parâmetros para personalizar/modificar o resultado de cada vez que a chamamos, as funções personalizadas podem incluir um ou parâmetros para as personalizar.
Assim, em vez de desenharmos sempre a mesma cabeça de lego, podemos personalizar (p. ex. ) a posição, o tamanho, etc.
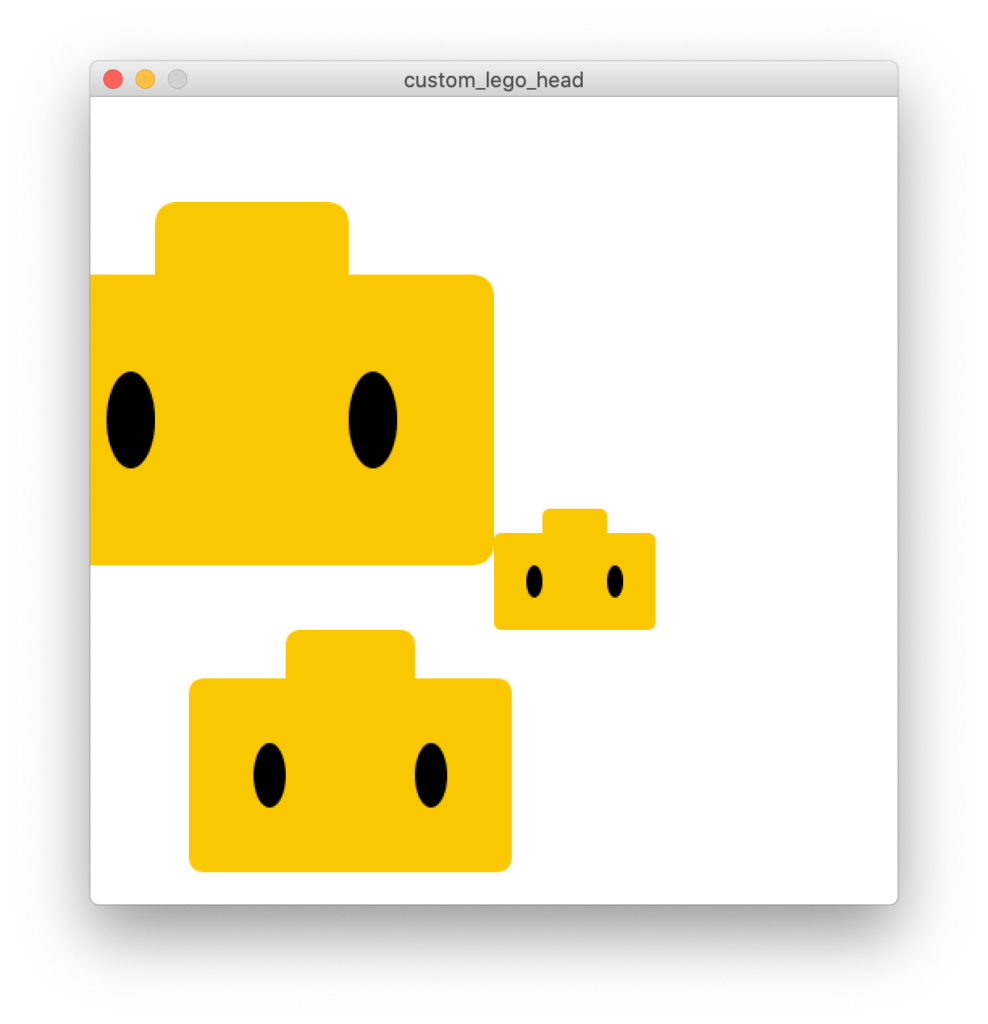
Para isso, incluímos valores (parâmetros) específicos dentro dos parêntesis da invocação da função:
// display
legoHead(100, 200, 1.5);
Cada um destes parâmetros vai ter que ter o seu correspondente na declaração da função. Isto é, imaginem uma ficha e uma tomada. Cada “perno” tem um “encaixe” correspondente. Isto é, na declaração da função (dentro dos parêntesis) declaram um número de variáveis com o tipo de dados correspondente para os receber, guardar e utilizar.
void legoHead(int x, int y, float s) { … }
Assim, quando a declaram, já sabem que vão receber um, dois, três ou mais valores da sua invocação. Estes valores vão servir para “personalizar” o resultados. Neste caso, o 100 transforma-se na variável x. O 200 transforma-se na variável y. E o 1.5 transforma-se na variável s. Reparem que o tipo de variável tem que corresponder ao tipo de dados/valores.
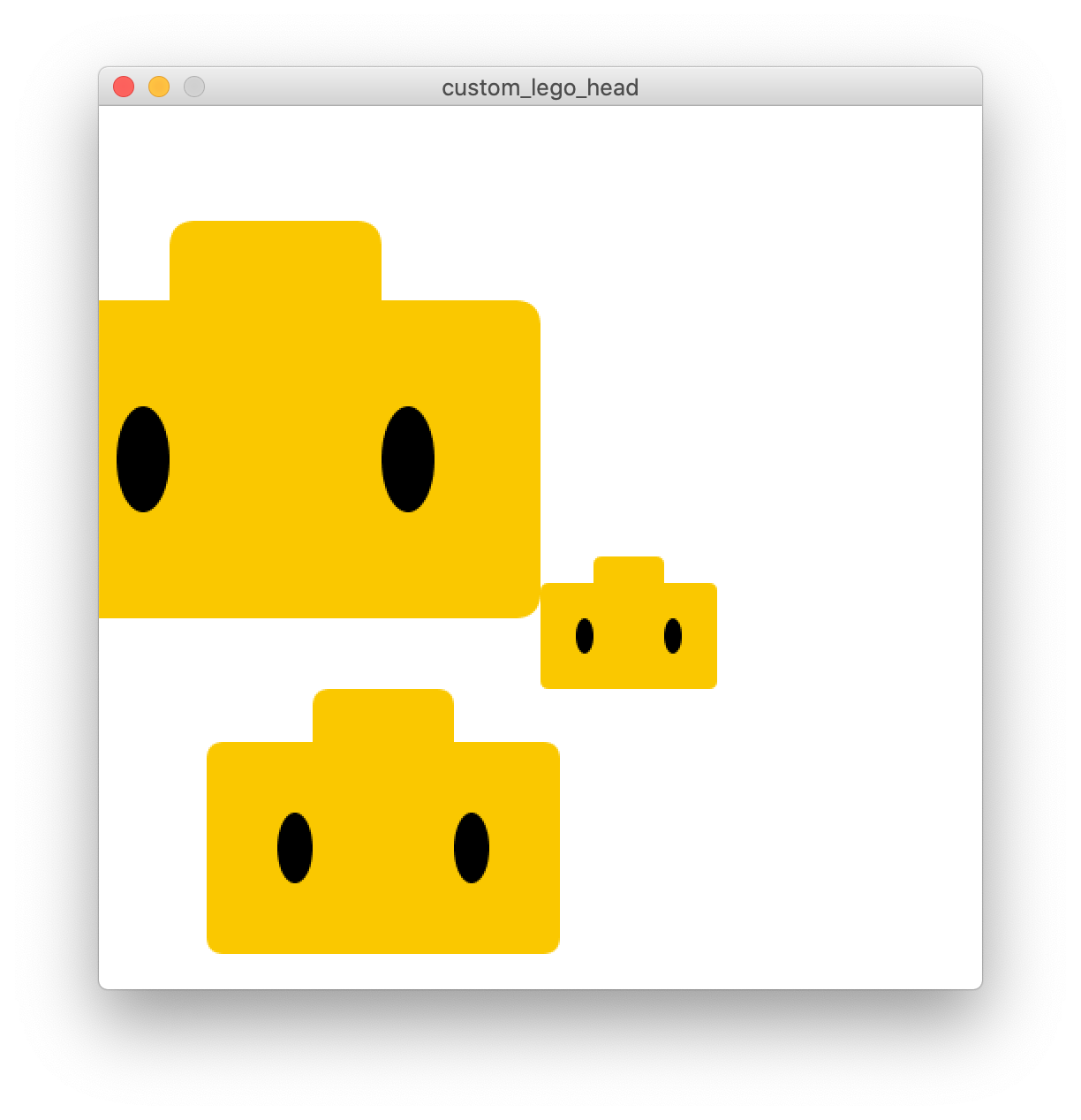
Então, é possível apenas com mais duas linhas de código “chamar” mais duas cópias inteiras da nossa cabeça de lego
// importar bibliotecas // Declarar objetos e variáveis // Inicializar void setup() { size(500, 500); background(255); noStroke(); rectMode(CENTER); } // Desenhar void draw() { // update background(255); // display legoHead(100, 200, 1.5); legoHead(300, 300, 0.5); legoHead(mouseX, mouseY, 1); } void legoHead(int x, int y, float s) { fill(250, 200, 0); rect(x, y, 200*s, 120*s, 10*s); fill(0); ellipse(x-50*s, y, 20*s, 40*s); ellipse(x+50*s, y, 20*s, 40*s); fill(250, 200, 0); rect(x, y-60*s, 80*s, 60*s, 10*s); }
Transformações
O segundo ponto da aula foram as transformações (mover, escalar e rodar objetos). A secção a estudar do reference é o Transform:
Estas funções permitem “congelar” (e guardar) o sistema de coordenadas do Processing para alterar temporariamente a forma como desenhamos. E, no final, voltar a repor tudo como estava. É como quando desenhamos em papel. Às vezes, é mais fácil mover e rodar o papel para desenhar um pormenor e depois voltamos a colocar a folha no sítio. É exatamente isto que o push e o pop fazem. Guardam a posição do “papel”, transformam as coordenadas — sempre por ordem loc, rot, scale — do “papel” do nosso sketch, permitindo-nos fazer alterações/transformações à forma como estamos a desenhar. e no fim repõem tudo como estava.
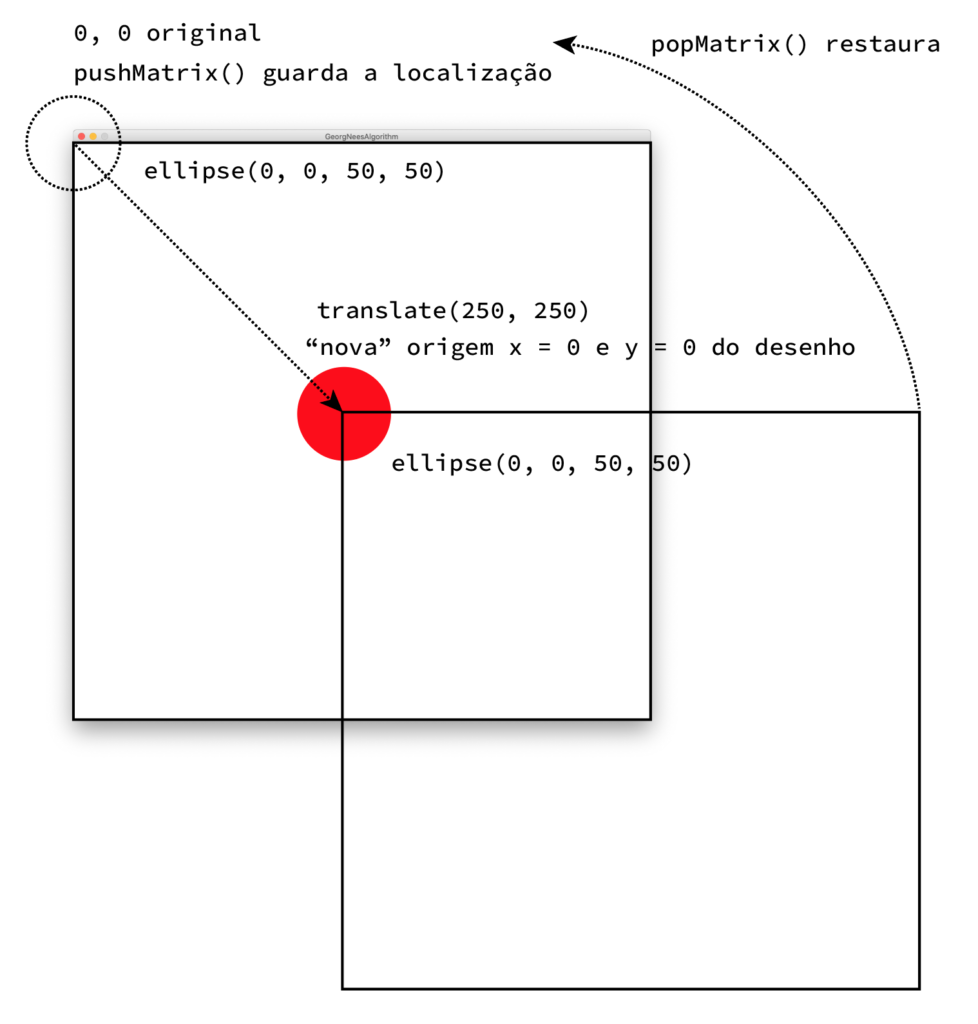
Na matriz de transformações, convém saber:
Expliquei isto com algum detalhe num post anterior: https://lsi.fba.up.pt/2019/2020/03/21/mais-uma-moeda-mais-uma-volta-todos-a-distancia-claro/. A informação mais importante a reter é que convém fazer estas transformações por esta ordem específica: Loc, Rot, Scale.
Mais algumas opções avançadas:
Coisas fixes ainda a ver :
Hoje (2021) a Beatriz mencionou que uma variável é como um estilo do InDesign. Adorei a analogia. É como uma referência que armazena as nossas escolhas, os nosso valores de cores, de tipografia, etc. Talvez esta seja a metáfora perfeita para um designer editorial compreender o que se passa numa variável. E, a oportunidade perfeita de aplicar isto é como o pushStyle() 😉
A piada deste tipo de transformações é que não se limitam ao sistema 2D. Para já, ainda não experimentamos, mas o Processing também trabalha com 3D. Quem quer fazer isto em 3D?
3D à parte, aproveitamos então para configurar o desenho da nossa cabeça de lego de forma muito mais fácil, com a transformação da matriz
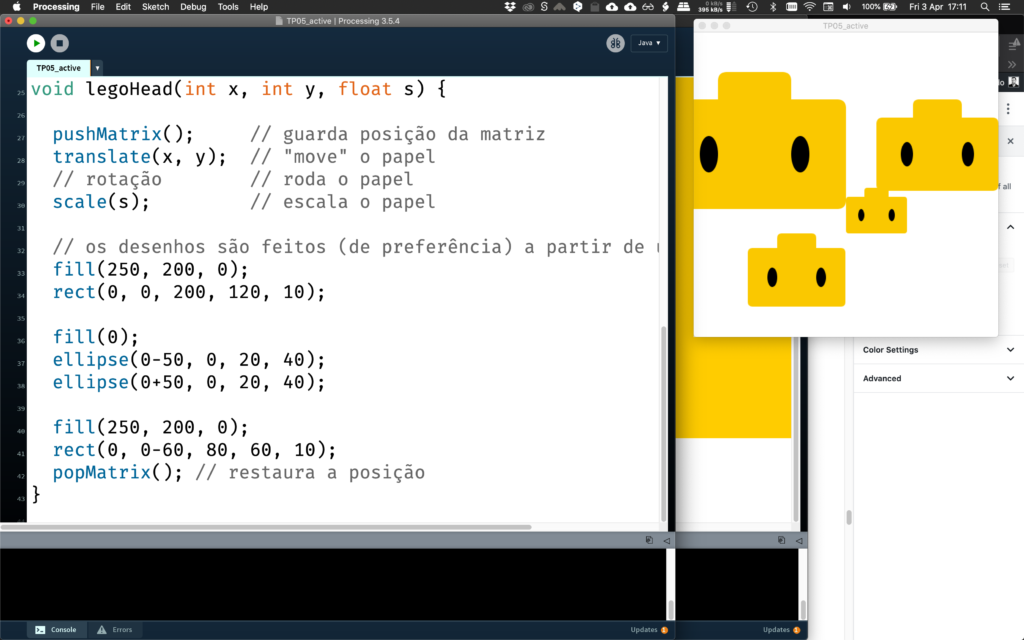
// importar bibliotecas // Declarar objetos e variáveis // Inicializar void setup() { size(500, 500); background(255); noStroke(); rectMode(CENTER); } // Desenhar void draw() { background(255); legoHead(100, 200, 1.5); legoHead(400, 200, 1.0); legoHead(300, 300, 0.5); legoHead(mouseX, mouseY, 0.8); } void legoHead(int x, int y, float s) { pushMatrix(); // guarda posição da matriz translate(x, y); // "move" o papel // rotação // roda o papel scale(s); // escala o papel // os desenhos são feitos (de preferência) a partir de um novo "zero" fill(250, 200, 0); rect(0, 0, 200, 120, 10); fill(0); ellipse(0-50, 0, 20, 40); ellipse(0+50, 0, 20, 40); fill(250, 200, 0); rect(0, 0-60, 80, 60, 10); popMatrix(); // restaura a posição }
Para demonstrar durante a aula, pegámos nos robôs (ou desenhamos um novo) e criámos uma círculo de em torno de um um ponto específico (variável).

// declaring variables & libraries int locX, locY; int n; // number of robots // prepare AKA initilize the program // this runs once void setup() { size(500, 500); background(255); //frameRate(12); locX = width/2; locY = height/2; n = 10; } // draw o run this function // automatically and continuosly void draw() { // don't forget to "clean" the screen for a new drawing background(255); //fill(255, 25); //noStroke(); //rect(0, 0, width, height); // draw an ellipse always on the mouse position noStroke(); fill(100); ellipse(mouseX, mouseY, 20, 20); // small tail stroke(0); noFill(); line(pmouseX, pmouseY, mouseX, mouseY); // this "calls" a function AKA a group or recipe or… module? //legoHead(100, 200, 150); // call the lego function with X and Y location // and then continues // circle of "n" robots for(int i = 0; i< n; i++) { pushMatrix(); translate(locX, locY); rotate( radians(i*(360/n) ) ); legoHead(150, 0, 150); popMatrix(); } } // this declares, or describes, or intructs how to draw this void legoHead(int x, int y, int w) { // function name (parameters inside) // lego robot head rectMode(CENTER); noStroke(); fill(250, 200, 0); rect(x, y, w, 50, 10); // head rect(x, y-20, w/3, 50, 10); // cucuruto fill(0); ellipse(x-20, y, 10, 20); // eyes ellipse(x+20, y, 10, 20); // eyes }
Vetores simples (arrays uni-dimensionais)
Nesta aula/ módulo ainda usamos (continuamos a usar) vetores… vamos continuar a falar sobre isto, por isso é importante relembrar novamente aqui os vetores (arrays) .
Um vetor é um tipo de variável composta / complexa. Na realidade é uma variável que, em vez de guardar apenas um valor, guarda um conjunto de valores diferentes. É como se fosse uma caixa de valores. normalmente explico isto da seguinte forma: um número é guardado numa caixa (variável). um conjunto de números é guardado numa caixa com várias posições como se fosse uma caixa de ovos. Tal como a caixa de ovos, o tipo de número, o tipo de variável é importante conhecer. Voltando à metáfora da caixa de ovos, um ovo de galinha (float) não cabe numa caixa de ovos de codorniz (int).
Agora que estou de volta disto, talvez uma metáfora de um comboio seja mais fácil de entender. As pessoas são os dados, os valores. Cada pessoa tem um lugar, um assento no comboio. Portanto, o assento é a variável que “guarda” o valor. Um vetor (array) simples é como uma carruagem de comboio simples que alinha, que permite ter uma fila de lugares. Portanto, podemos ter por exemplo 10 pessoas (valores) na carruagem. No lugar um, o José. No lugar dois, a Maria. E por aqui fora.
Os vetores então permitem (pré)conhecer todos os valores antes de desenhar. E, deste modo, permite-nos calcular posições, interações e desenhar formas com todos estes valores.
Tal como num módulo anterior, nós podemos querer desenhar um número indeterminado (que cresce ou que diminui) de elementos no ecrã. E que podemos querer liga-los entre si (para desenhar, ou para calcular posições). Para isso, dá-nos muito jeito saber manipular vetores (arrays).
O exemplo que se segue, demonstra isto mesmo, tentando criar um efeito de uma “cauda”, ou um efeito semelhante daquele jogo antiguinho dos Nokias — o nibbles ou o snake?
Isto só é possível sabendo e utilizando todas as posições de antemão.
Para isso, criamos uma lista de posições — um vetor — para todas as posições horizontais e verticais das bolas. Em cada ciclo de draw, fazemos um loop (de trás para a frente) em que dizemos que a posição da última coordenada das listas é igual à penúltima. A penúltima é igual a ante-penúltima. E por aqui fora até à primeira posição. Chegando à primeira, esta segue a posição do rato.
Assim que temos todas as posições atualizadas, basta desenhar bolas e linhas nas posições da(s) lista(s).
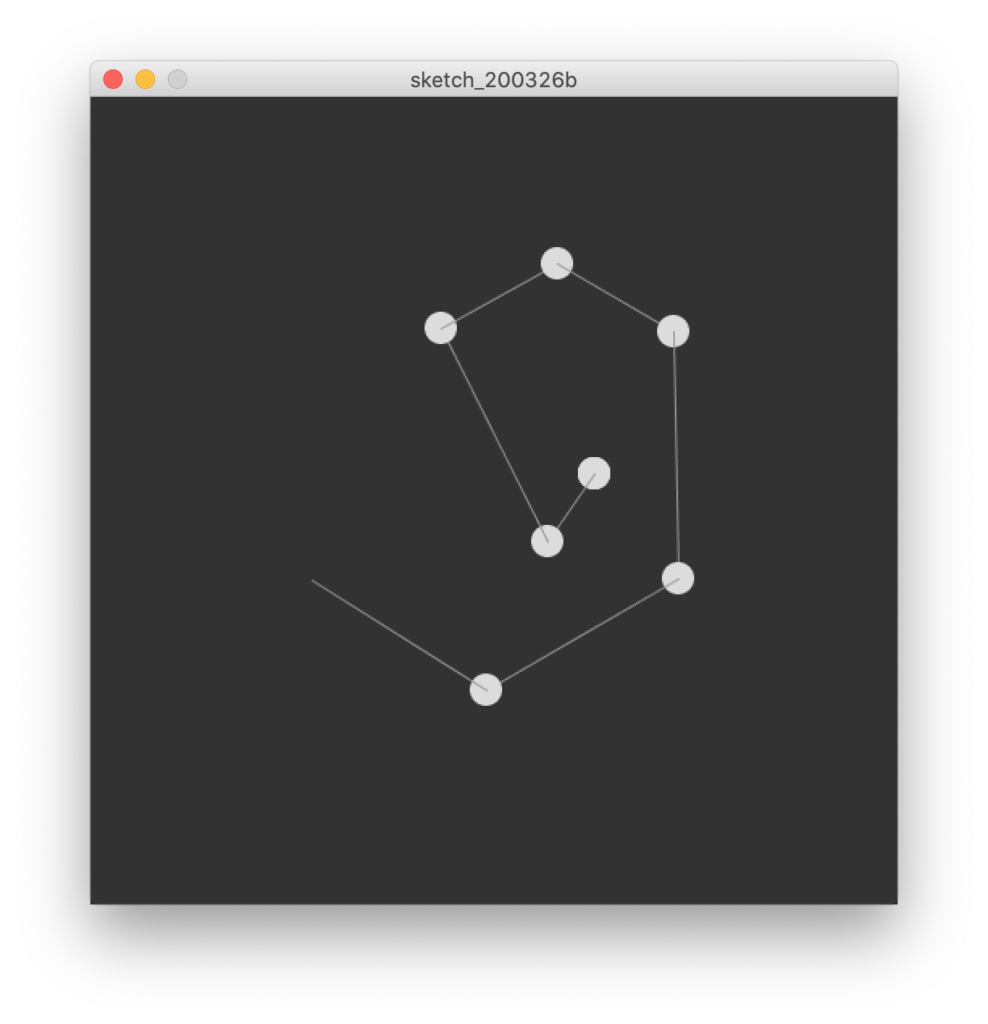
// declarar int[] locX, locY; int n; // inicializar void setup() { size(500, 500); frameRate(5); n = 10; locX = new int[n]; locY = new int[n]; for (int i = 0; i < n; i++) { locX[i] = i*30 + 100; locY[i] = 100; } } // desenhar void draw() { background(50); // update for (int i = n-1; i > 0; i--) { locX[i] = locX[i-1]; locY[i] = locY[i-1]; } locX[0] = mouseX; locY[0] = mouseY; // draw for (int i = 0; i < n-1; i++) { noStroke(); fill(220); ellipse( locX[i], locY[i], 20, 20); noFill(); stroke(150); line(locX[i], locY[i], locX[i+1], locY[i+1]); } }
Aqui ficam algumas funções relativamente fáceis de entender… (vamos usar na próxima aula)
É importante conhecer a sintaxe de declaração da variável de um vetor. Começa com o tipo, seguido de dois parêntesis retos (a “caixa”), seguido do nome da variável.
// declare int[] locX;
Segue-se a sua “construção”. As variáveis complexas têm que ser construídas antes de serem inicializadas/populadas
n = 10; // initialize ne number of items locX = new int[n]; // contrstuc the array
E depois inicializamos cada um dos valores do vetor
for (int i=0; i < n; i++) { // initialize each position inarray locX[i] = -100; }
Aqui é importante conhecer a sintaxe de índice de acesso dos valores do array para poder aceder (ler), utilizar e modificar cada valor específico que foi armazenado.
Array Functions
Recomendo ver estas primeiro porque são muito práticas e de uso imediato neste projeto. De seguida (para projetos diferentes, por exemplo para desenho de infografia e gráficos)
E de resto, convém sempre saber que existem pelo menos. Vai chegar o dia em que vamos precisar de
Este desafio foi ainda estendido com:
- os robôs devem “orbitar” automaticamente (devem girar em torno do rato como se fossem satélites)
Embora se consiga fazer de forma relativamente fácil com a transformação da matriz e funções parametrizadas, muito mais giro vai ser conhecer e utilizar a secção de Matemática/trigonometria do reference, nomeadamente:
Trigonometry
Em 2019, como exercício/demonstração/aplicação de todos os conceitos da(s) aula(s) criámos um “mini-jogo” onde um esquadrão de 10 Tie-fighters (interceptors) perseguem um X-Wing. Numa primeira instância desenhámos como se fosse o jogo Snake (nibbles) dos Nokia (lembram-se?). Onde cada objeto segue “religiosamente” o caminho do seu objeto anterior.
Depois passamos a modo “voltas no ginásio de educação física do liceu”. Onde cada objeto vai seguindo o anterior, mas “corta as curvas”. Dá um efeito mais orgânico.

// declare int[] locX, locY; int n; PImage xing, tie; void setup() { size(1000, 500); //frameRate(10); background(255); n = 10; // initialize ne number of items locX = new int[n]; // contrstuc the array locY = new int[n]; for (int i=0; i < n; i++) { // initialize each position inarray locX[i] = -100; locY[i] = -100; } rectMode(CENTER); imageMode(CENTER); xing = loadImage("x-wing-1.png"); tie = loadImage("tie-interceptor-1.png"); } void draw() { background(255); stroke(50); noFill(); //triangle(mouseX-30, mouseY, mouseX+10, mouseY-10, mouseX+10, mouseY+10); image(xing, mouseX, mouseY, 90, 60); // update positions (almost all) for (int i=n-1; i > 0; i--) { // loop through all them backwards locX[i] = locX[i] + (locX[i-1]-locX[i])/9; locY[i] = locY[i] + (locY[i-1]-locY[i])/9;; } // dont forget the 1st one locX[0] = pmouseX; locY[0] = pmouseY; // display the elements for (int i=1; i < n; i++) { // loop draw through them fill(255, 0, 0, 255-i*5); noStroke(); //ellipse(locX[i], locY[i], 30, 20); image(tie, locX[i], locY[i], 55, 35); if (i < n-1) { stroke(0); strokeWeight(1); line(locX[i], locY[i], locX[i+1], locY[i+1]); } } } void keyPressed() { strokeWeight(10); stroke(255, 0, 0); line(locX[0], locY[0], locX[1], locY[1]); }
Em 2019, na turma da tarde ainda deu tempo para começarmos a ver os eventos e criar um ligeiro efeito de “tiros” de blaster quando se carrega na barra de espaços! 😉
O desafio “extra-extra” consiste em orientar (o ângulo e a direção) das naves mediante o percurso/perseguição que vão fazer. Para isso, devem ligar todos os conceitos até agora — pushMatrix vai ser muito útil. Muito útil também vai ser a seção de Matemática/trigonometria do reference novamente:
Trigonometry
O atan2() é fndamental nesta altura. Pelo menos, enquanto não chegamos aos objetos realmente interessantes, como o PVector (que tem estas coisas incorporadas!)
Era espetacular que — Xtra 2: When X-Wings cover great[er] distances, they change wing pattern design (closed / X-wing).
Gostava de transformar isto num “space blocade”. Isto é, ter uma série de star destroyers a orbitar um planeta e os tie-fighters/x-wings a voarem entre eles… alguém se voluntaria?
Mesmo no fim, aplicámos estes exemplos a uma demonstração de Motion Graphics / Dynamic Typography como o trabalho do Dia Studio com uma faixa a ser animada/distorcida

// declare int[] locX, locY; int n; PImage img1, img2, img3; // regular images PImage img1i, img2i, img3i; // inverted void setup() { size(1000, 500); //frameRate(10); background(255); n = 4; // initialize ne number of items locX = new int[n]; // contrstuc the array locY = new int[n]; for (int i=0; i < n; i++) { // initialize each position inarray locX[i] = -100; locY[i] = -100; } rectMode(CORNERS); img1 = loadImage("disru.jpg"); img2 = loadImage("pti.jpg"); img3 = loadImage("on.jpg"); img1i = loadImage("disru-i.jpg"); img2i = loadImage("pti-i.jpg"); img3i = loadImage("on-i.jpg"); } void draw() { background(255); // update positions (almost all) for (int i=n-1; i > 0; i--) { // loop through all them backwards locX[i] = locX[i] + (locX[i-1]-locX[i])/9; locY[i] = locY[i] + (locY[i-1]-locY[i])/9; ; } // dont forget the 1st one locX[0] = pmouseX; locY[0] = pmouseY; // display the elements for (int i=0; i < n; i++) { // loop draw through them fill(100); noStroke(); ellipse(locX[i], 200, 10, 10); ellipse(locX[i], 300, 10, 10); } if (locX[0] <= locX[1]) { image(img1, locX[0], 100, locX[1]-locX[0], 300); } else { image(img1i, locX[0], 100, locX[1]-locX[0], 300); } if (locX[1] <= locX[2]) { image(img2, locX[1], 100, locX[2]-locX[1], 300); } else { image(img2i, locX[1], 100, locX[2]-locX[1], 300); } if (locX[2] <= locX[3]) { image(img3, locX[2], 100, locX[3]-locX[2], 300); } else { image(img3i, locX[2], 100, locX[3]-locX[2], 300); } }
Estes desafios, à semelhança de alguns projetos/ideias anteriores, precisam de usar alguns cálculos de matemática. Nada demais, coisas do dia-a-dia, mas que o Processing implementa de forma relativamente simples. Coisas como saber se a distância é maior ou menor que um valor — nós fazemos isto automaticamente na cabeça —, mas o processing precisa de uma ajuda. Por exemplo, se o objeto estiver para a direita a distância é positiva, mas se estiver para a esquerda a distância é negativa (e já não conseguimos fazer a verificação de forma tão simples… ou talvez…)
Por isso dá jeito conhecer a secção de cálculos do reference. Especialmente o abs() — valor absoluto (converte positivos e negativos sempre no valor absoluto/positivo) —, e o dist() — que calcula o valor absoluto do vetor de distância entre dois pontos.
Calculation
E, claro, pelo menos saber que estão lá para quando precisarmos deles
Enfim. Resumindo o modo ativo, vamos trabalhar sempre da seguinte forma:
- Importar Bibliotecas;
- Declarar
- Objetos,
- Variáveis;
- Inicializar
- programa,
- objetos e
- variáveis;
- Desenhar
- update
- display
- Eventos
- Keyboard
- Mouse
- Etc…
- Saída (on special occasions must deal with exit() )
- Funções adicionais (personalizadas)
- Objetos adicionais
No final do dia, o desafio é:
Exercício 3:
Make 3 robots circle a fourth… or better yet, make three star destroyers circle around Aalderaan
Exercício 3: Extra
Make 3 tie fighers circle each star destroyer. Make each ship avoid the mouse (eg. 100 px radius)
Este artigo é um documento em progresso. Editado 2019-03-29, 2020-04-03, 2021-02-25