Segunda semana de contenção e isolamento. As aulas online continuam a decorrer com o Colibri-Zoom. Desta feita com uma assistência ligeiramente maior do que na semana passada (mas não tão popular como as aulas de tipografia ou desenho de tipos!)
Durante a manhã, deu para (re)ver alguns trabalhos em processo. De uma forma global, todos estudantes parecem estar a compreender o objetivo, pesquisar autores e a realizar obras gráficas interpretativas a partir do espólio / estilo gráfico estudado.
- Fizemos (começámos na aula e acabei aqui) uma distorção polar simples, baseada no trabalho de Victor Vasarely usando cálculos novos (abs e map);
- Continuamos uma ideia de uma máquina de desenho baseada no Georg Nees, utilizando trigoometria para calcular rotaçõs e o pushMatrix (parece que todos querem rodar e transformar os desenhos este ano!)
Durante a tarde vimos novamente uma série de exemplos porreiros mas o mais entusiasmante foi — novamente um desafio — criar uma espécie de padrão de linha ondulante de calçada portuguesa (ou calçadão do leblon?).
Novamente, numa rápida sessão de “live-coding”, usamos a trigonometria para explicar o movimento ondulatório. As dúvidas deste ano estão a puxar muito para a geo-trigono-metria 😉

Desta vez apenas tivemos um problema com um dos microfones durante a sessão. Ainda assim o modo de texto ajudou. O que foi um pouco irritante, porque a dúvida que a estudante colocou — a Ana Leite — era muito fixe e demorou um pouco a resolver.
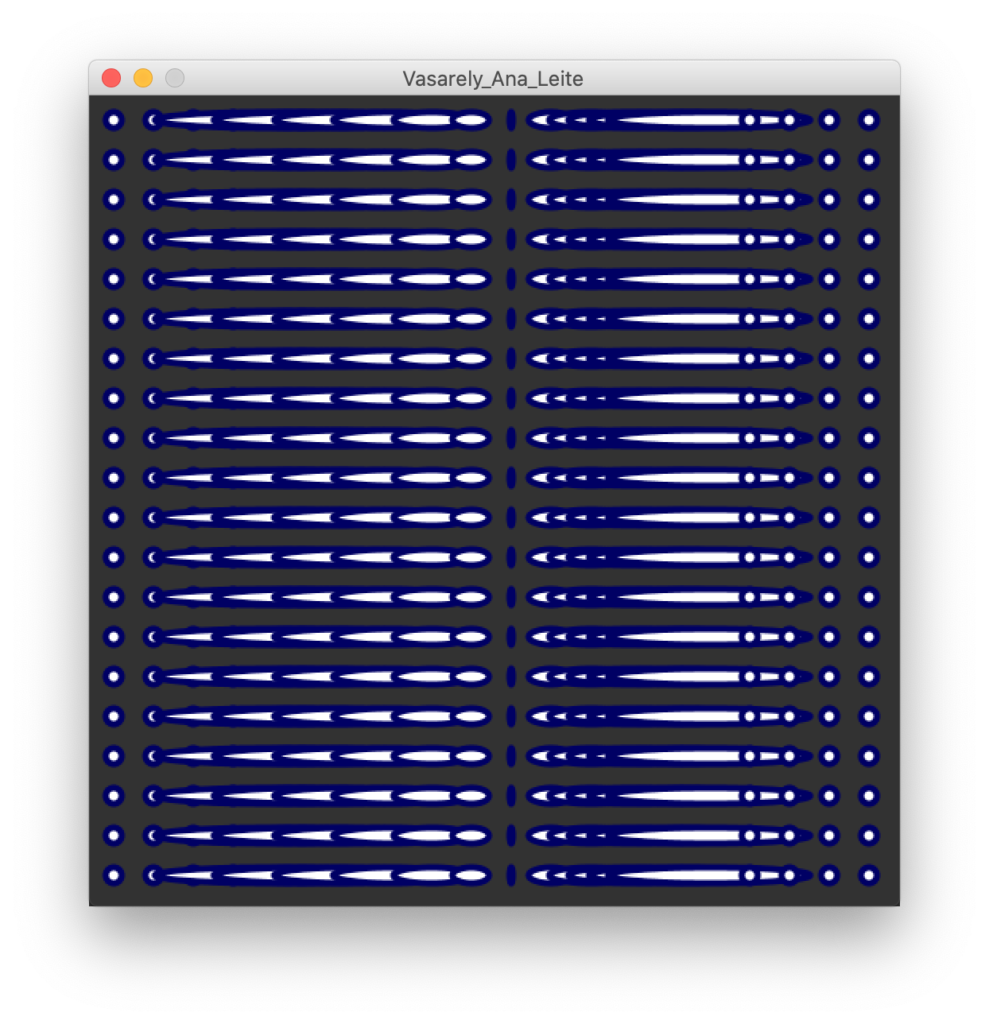
O trabalho original dela é um retrato do Victor Vasarely. As cores ainda estão um pouco-psicadélicas (prefiro de longe o segundo), mas o interessante ver foi o algoritmo de afastamento (displacement) dos “pixels”.

Victor Vasarely por Ana Leite

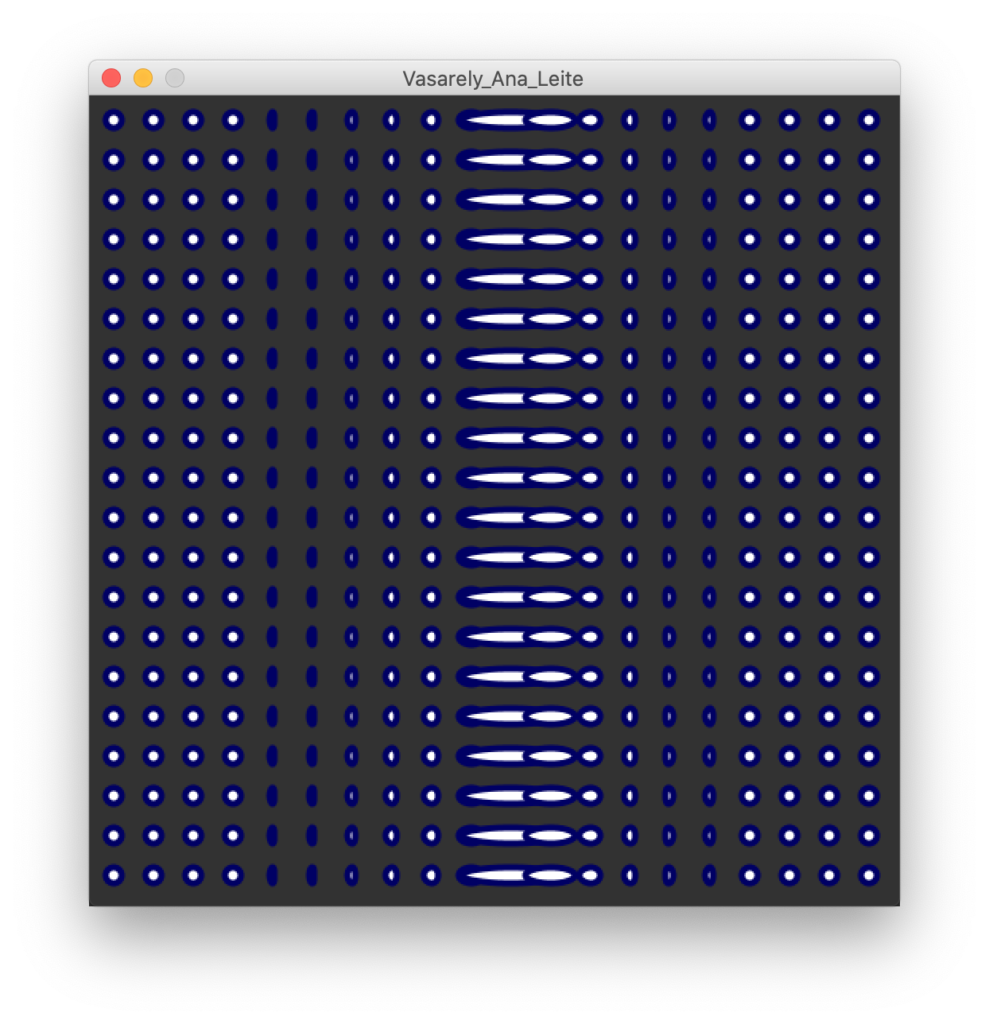
O aspeto mais interessante e original nestes três anos de Processing foi usar a cor para fazer a transformação espacial do pixel (primeira abordagem). Apesar de não ter sido intencional, a Ana está, de certa forma, a usar o valor da cor para decidir a altura do pixel. Quase como se fosse um depth map. Mais à frente percebi que ela estava à procura de uma espécie de “lenticularização” , uma distorção de coordenadas polar.

Ainda tentámos adaptar o código dela, mas o tempo não deu para muito. Deu para fazer o básico, mas acho que a mensagem não passou bem. O código dela já estava muito confuso (e o uso do scale() não estava a permitir ver as mudanças da melhor forma).
Isto é um algoritmo relativamente simples de implementar. Isto é, nesta fase do campeonato, sem complicar muito, apenas com ifs e sem grandes variáveis complexas (como arrays bi-dimensionais que vamos ver para a semana), é possível fazer com algum esforço de lógica e compromisso visual. Aqui vai uma tentativa rápida. Primeiro começamos com um loop simples:

// PAmado, 2020-03-21 // A partir da interpretação de Ana Leite / Victor Vasarely // declare variables int ballSize; int spacing; // Setup sketch size(510, 510); background(50); // initialize variables ballSize = 20; spacing = 5; // draw translate(15, 15); // move the page a bit to the left (to get the drawing more centered) // do the loop with the shapes for (int i = 0; i < 20; i++) { for (int k = 0; k < 20; k++) { int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); stroke(0, 0, 100); strokeWeight(4); ellipse(x, y, ballSize, ballSize); } }
Depois passamos ao algoritmo. A ideia de fazer uma distorção de coordenadas polares (pinch ou zoom) é, basicamente: quanto mais perto do centro (de distorção) estiver cada uma dessas formas, mais essa distância afeta a sua geometria. Temos é que nos lembrar que é uma razão invertida. Isto é, quanto menor a distância, maior a distorção.
Passamos ao exemplo, apenas com as coordenadas horizontais. Neste sketch tive necessidade de usar algumas operações de cálculo. Nomeadamente o abs().
// calculate the position int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); // check if the position is within the distortion boundaries int dx = cx-x; // check the distance (delta) between current x and the polar center int w = ballSize/2; // calculate new dimensions if ( abs(dx) < boundaries ) { /* here we are using abs() to get the absolute (positive) number . You can also use dist() */ w = dx; }
Neste exemplo, a coisa está estranha, pois nós apenas usamos a distância ao centro (se estiver dentro do raio de distorção pretendido) e usamos o próprio valor de distância para distorcer. Mas, se usarmos um map(), podemos inverter a grandeza e mapear imediatamente para um valor/fator de escala mais utilizável (sei que isto nesta fase é capaz de ser um pouco cedo/rápido/complexo, mas na realidade já expliquei isto pelo menos a 3 estudantes… quanto mais cedo, melhor?)
// PAmado, 2020-03-21 // A partir da interpretação de Ana Leite / Victor Vasarely // declare variables int ballSize; int spacing; int offset; // this will be used to center drawing on stage int cx, cy; // this will be the center of the distortion target int boundaries; // Setup sketch size(510, 510); background(50); // initialize variables ballSize = 20; spacing = 5; offset = 15; cx = width/2 - offset/2; cy = height/2 - offset/2; boundaries = 150; // draw translate(offset, offset); // move the page a bit to the left (to get the drawing more centered) // do the loop with the shapes for (int i = 0; i < 20; i++) { for (int k = 0; k < 20; k++) { // calculate the position int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); // check if the position is within the distortion boundaries int dx = cx-x; // check the distance (delta) between current x and the polar center float w = ballSize/2; // calculate new dimensions float fx = 1; if ( abs(dx) < boundaries ) { /* here we are using abs() to get the absolute (positive) number . You can also use dist() */ fx = map(dx, 0, boundaries*2, 0.2, 6); } stroke(0, 0, 100); strokeWeight(4); ellipse(x, y, w/fx, ballSize/2); // always draw the ball with the size * scale factor. Dont' forget to invert the scaling: bigger as distance is shorter } }
E é isto. A partir daqui é curtir as cores e o formato dos pixels, usando as coordenadas horizontais e verticais.
A primeira abordagem dá resultados meios freaks…
Por isso, está na altura de experimentar o dist()
float w = ballSize/2; // calculate new dimensions float fx = 1; float fy = 1; if ( dist(cx, cy, x, y) < boundaries ) { /* changed into dist() instead of abs to calculate both*/ fx = map(dx, 0, boundaries, 0.5, 10); fy = map(dy, 0, boundaries, 0.5, 10); } stroke(0, 0, 100); strokeWeight(4); ellipse(x, y, w/fx, w/fy); // always draw the ball with the size * scale factor. Dont' forget to invert the scaling: bigger as distance is shorter }
Et voilá. Não ficou exatamente igual, mas já está a trabalhar. Para um sketch rápido não ficou nada mal. Agora é brincar com o fator de escala de uma forma mais suave ou progressiva e ligar este fator a um desfasamento espacial.
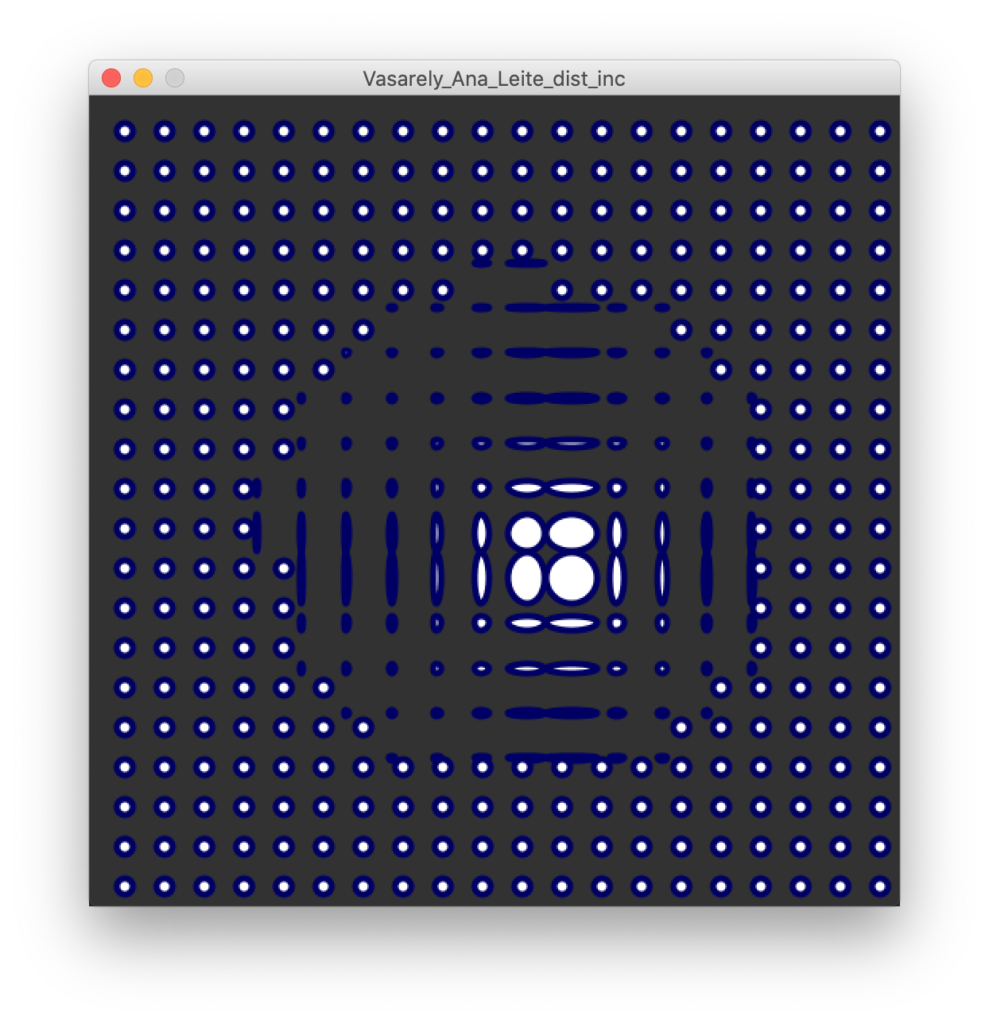
// PAmado, 2020-03-21 // A partir da interpretação de Ana Leite / Victor Vasarely // declare variables int ballSize; int spacing; int offset; // this will be used to center drawing on stage int cx, cy; // this will be the center of the distortion target int boundaries; // Setup sketch size(510, 510); background(50); // initialize variables ballSize = 20; spacing = 5; offset = 15; cx = width/2 - offset/2; cy = height/2 - offset/2; boundaries = 150; // draw translate(offset, offset); // move the page a bit to the left (to get the drawing more centered) // do the loop with the shapes for (int i = 0; i < 20; i++) { for (int k = 0; k < 20; k++) { // calculate the position int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); // check if the position is within the distortion boundaries float dx = cx-x; // check the distance (delta) between current x and the polar center float dy = cy-y; // check the distance (delta) between current x and the polar center float w = ballSize/2; // calculate new dimensions float fx = 1; float fy = 1; if ( dist(cx, cy, x, y) < boundaries ) { /* changed into dist() instead of abs to calculate both*/ fx = map(dx, 0, boundaries, 0.5, 5); fy = map(dy, 0, boundaries, 0.5, 5); } stroke(0, 0, 100); strokeWeight(4); float incx = map(fx, 0.5, 5, ballSize/2, -ballSize/2); float incy = map(fy, 0.5, 5, ballSize/2, -ballSize/2); ellipse(x + incx, y + incy, w/fx, w/fy); // always draw the ball with the size * scale factor. Dont' forget to invert the scaling: bigger as distance is shorter } }
Continuando uma ideia que tinha vindo já da aula anterior/troca de emails a pedido da Maria Jorge, voltámos às transformações pushMatrix() e à trigonometria que foi a coisa mais divertida que estivemos também a fazer durante a aula da tarde (e que vamos ver na próxima aula).
Podem rever a (re)construção deste algoritmo a partir das 02h48′ da gravação da aula. Por isso não vou estar aqui a explicar em grande detalhe. O objetivo é fazer “bolas” com segmentos de reta unidos entre si. Algo assim:
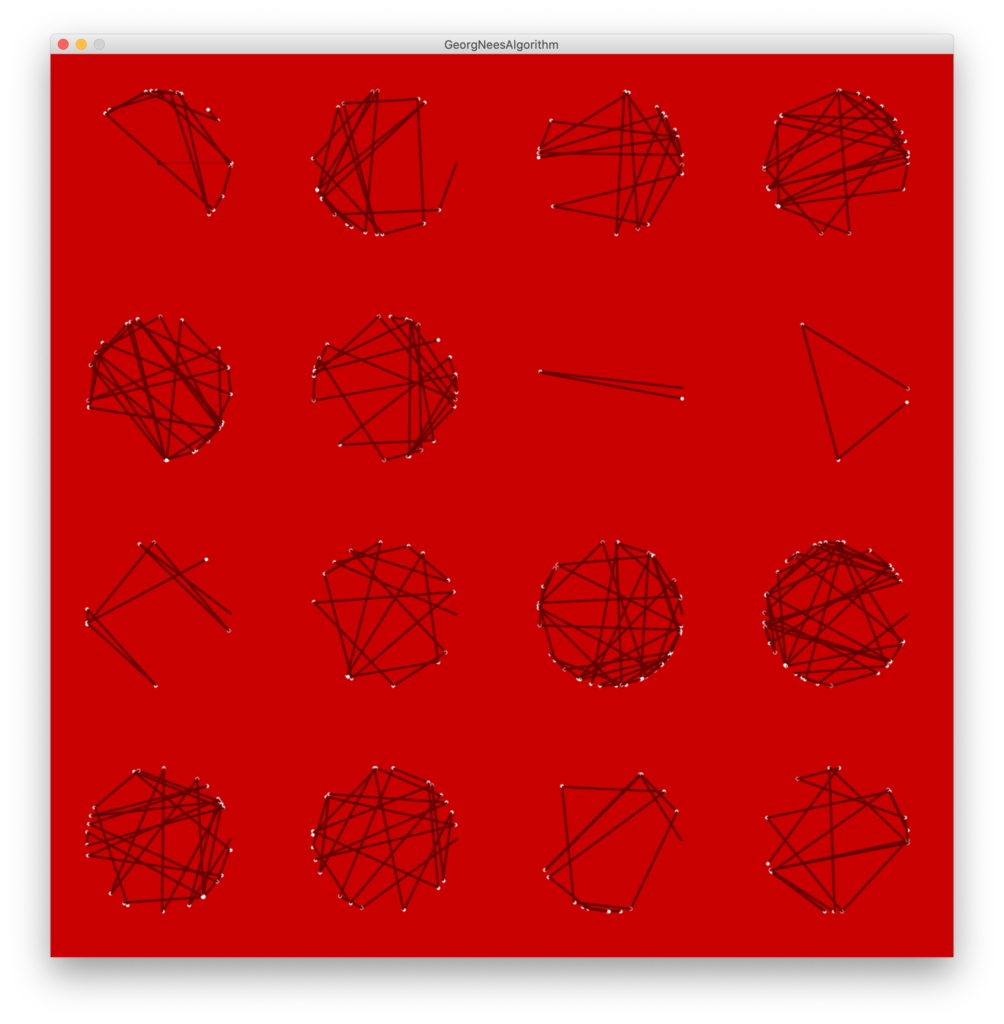
Para isso começamos com o nosso nested loop do costume…
for ( int m = 0; m < 4; m++) { for ( int n = 0; n < 4; n++ ) { // draw here… } }
Quando desenharmos os círculos, o objetivo é “ir buscar a cor de cada pixel de uma imagem de um retrato”. E desenhar tantas linhas conforme a intensidade (brilho) desse pixel. No exemplo, usámos valores aleatórios.
// desenhos dos circulos int loop = int( random(50) +2); // <-- modifica este para a cor…
A seguir convém entender como funciona um transform no Processing. Vamos usar um pushMatrix() para o Processing “congelar” na memória a posição do desenho (da “folha” de papel do sketch). Depois usamos — por ordem loc rot scale — as transformações de espaço translate(), de rotação rotate() e de escala scale() para posicionar o nosso desenho onde queremos. Isto é, não é o “braço” de desenho que se “mexe” mas sim, o suporte. Na prática, isto “move” o sistema de coordenadas absolutas do Processing. E, quando desenhamos, desenhamos (de preferência) a partir do ponto 0, 0. Ou seja, a partir da nova origem. Isto permite não são desenhar mais facilmente (temos que desenhar como quando modelamos em 3D, com coordenadas relativas a partir deste centro / pivot novo). Mas temos que nos lembrar de, no fim, restaurar o sistema de coordenadas com o popMatrix().
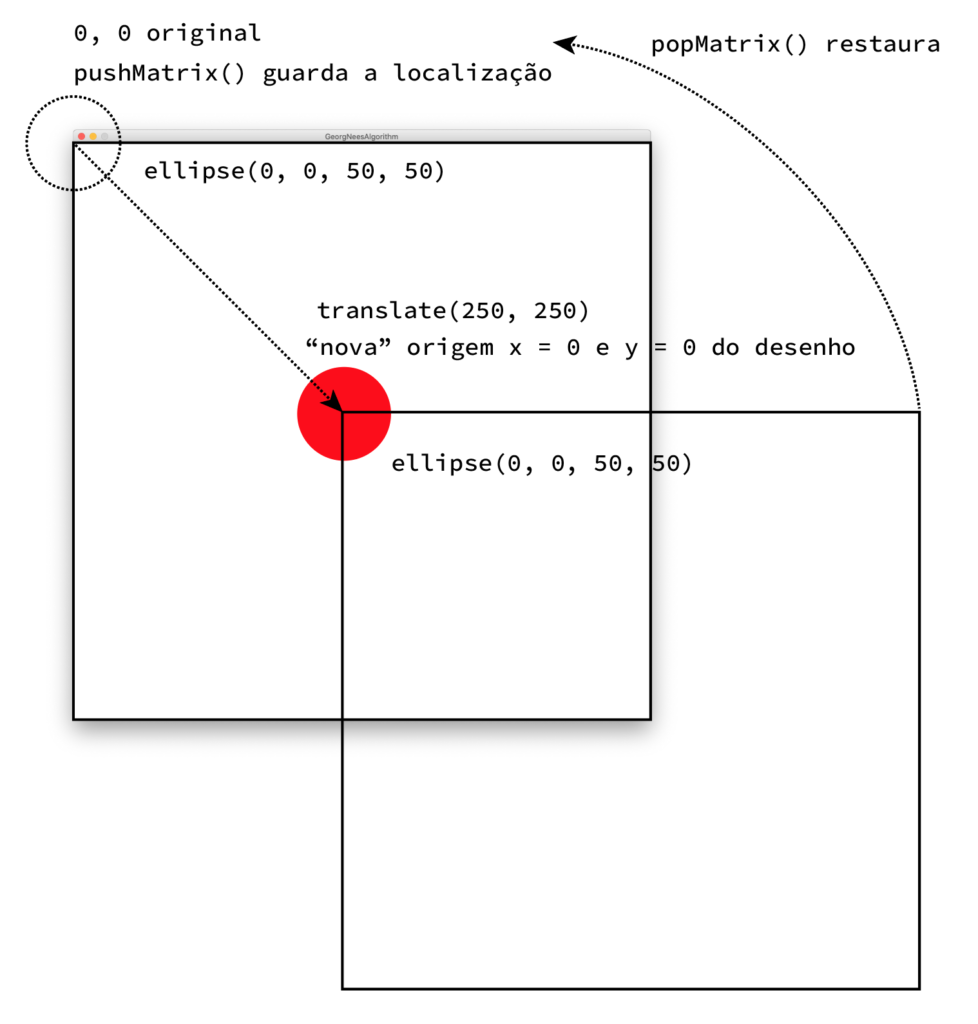
Nós vamos fazer esta movimentação tantas vezes quantas as que são necessárias para desenhar as bolas do Nees (nested loop anterior).
pushMatrix(); translate(m*250, n*250); // draw here… popMatrix();
E depois passamos à questão da trigonometria. Para desenhar qualquer ponto num perímetro de uma circunferência temos que nos lembrar de matemática do… 7.º ano?… É naquela altura em que se fala do [teorema de] pitágoras… 😉
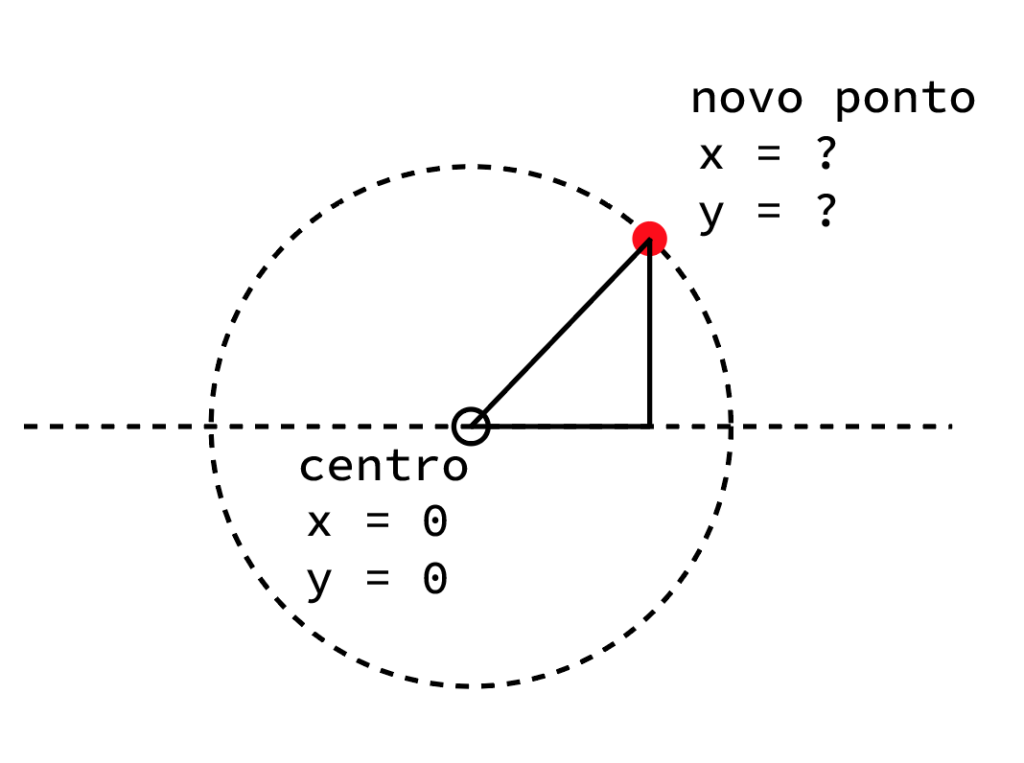
Uma vez que sabemos “onde estamos” (o centro do desenho) e o tamanho da circunferência que queremos (o raio), só nos falta desenhar com um ângulo qualquer um novo ponto no perímetro da circunferência. E para isso, usamos as expressões da trigonometria: novo x = raio * coseno (ângulo); novo y = raio * seno (ângulo);
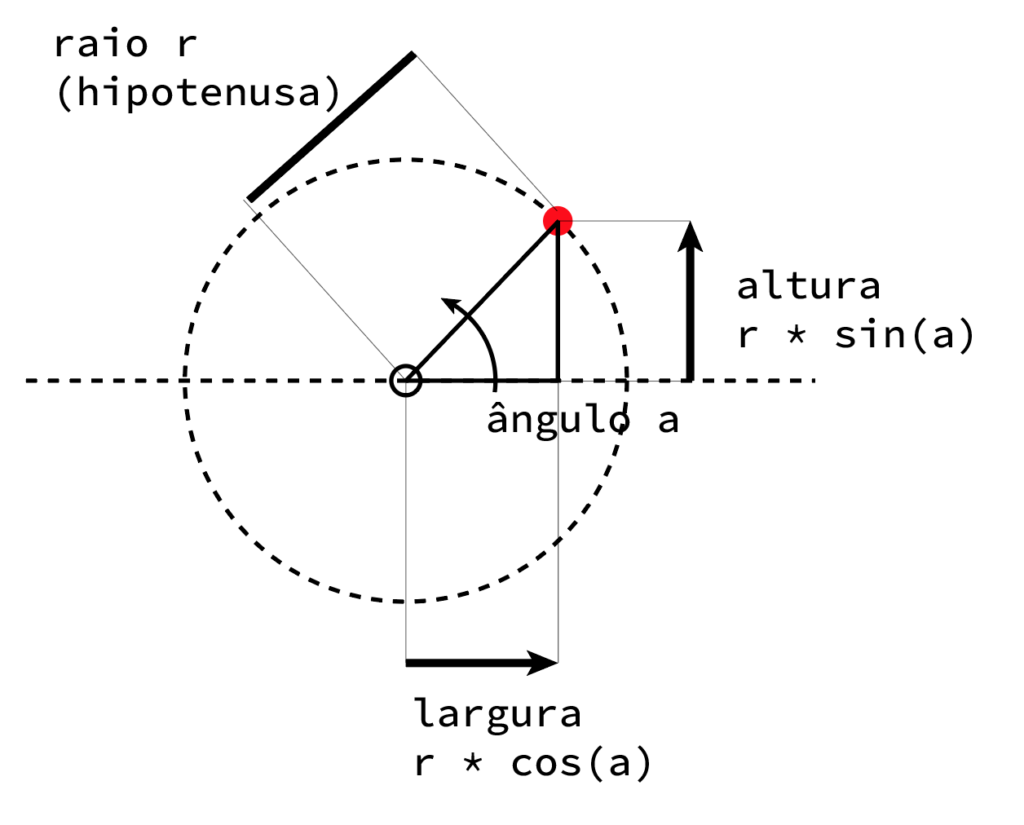
Portanto é fácil desenhar qualquer ponto com esta fórmula. Todos os novos pontos na circunferência são iguais ao centro original + raio*sen / cos do angulo pretendido.
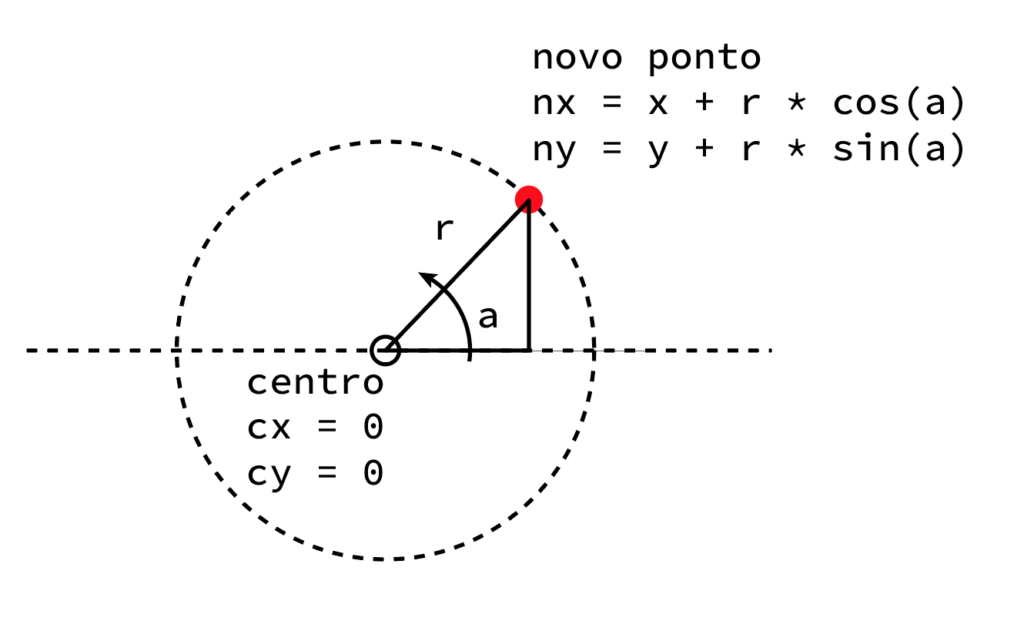
Rinse and repeat tantas vezes quanto necessárias. Só falta mais um truque. Queremos desenhar linhas de um ponto (de um ângulo) para outro (novo ângulo). Por isso vamos recorrer às nossas velhinhas variáveis para guardar a última posição (ângulo) e, sempre que calculamos um ângulo novo, “rodamos o ângulo anterior para trás” e desenhamos a linha do ponto velho, para o ponto novo.
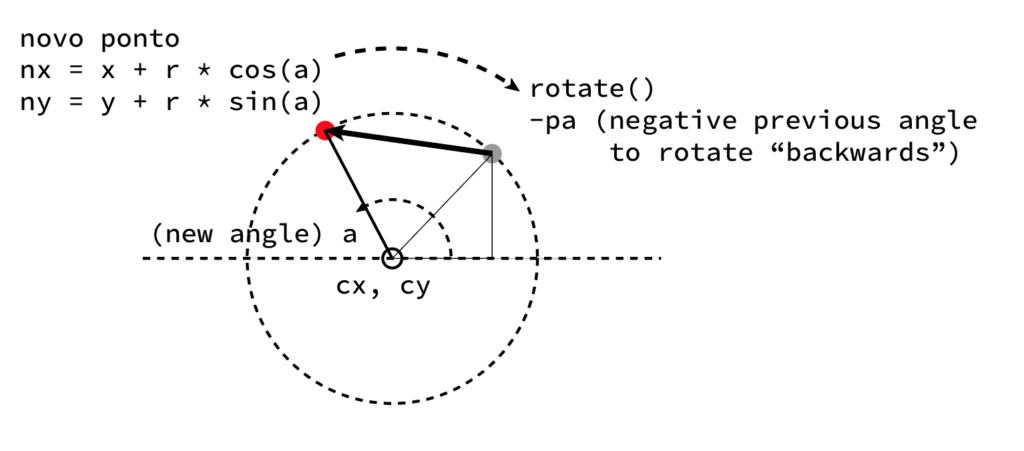
Mas temos que nos lembrar que estávamos a usar um pushMatrix dentro de um loop, e por isso torna-se um pouco complicado “voltar atrás”. Quer dizer… bom, na quinta-feira passada fizemos assim, não quer dizer que seja a forma mais fácil de fazer. Mas foi a mais rápida… Por isso, temos que pensar que é o “papel” que roda e não o desenho em si.
Por isso, sempre que rodamos, guardamos ângulo. Ao rodar novamente, acrescentamos uma rotação no sentido inverso com o ângulo anterior (para recuperar as coordenadas do ponto que precedeu) e desenhamos uma linha entre os dois.
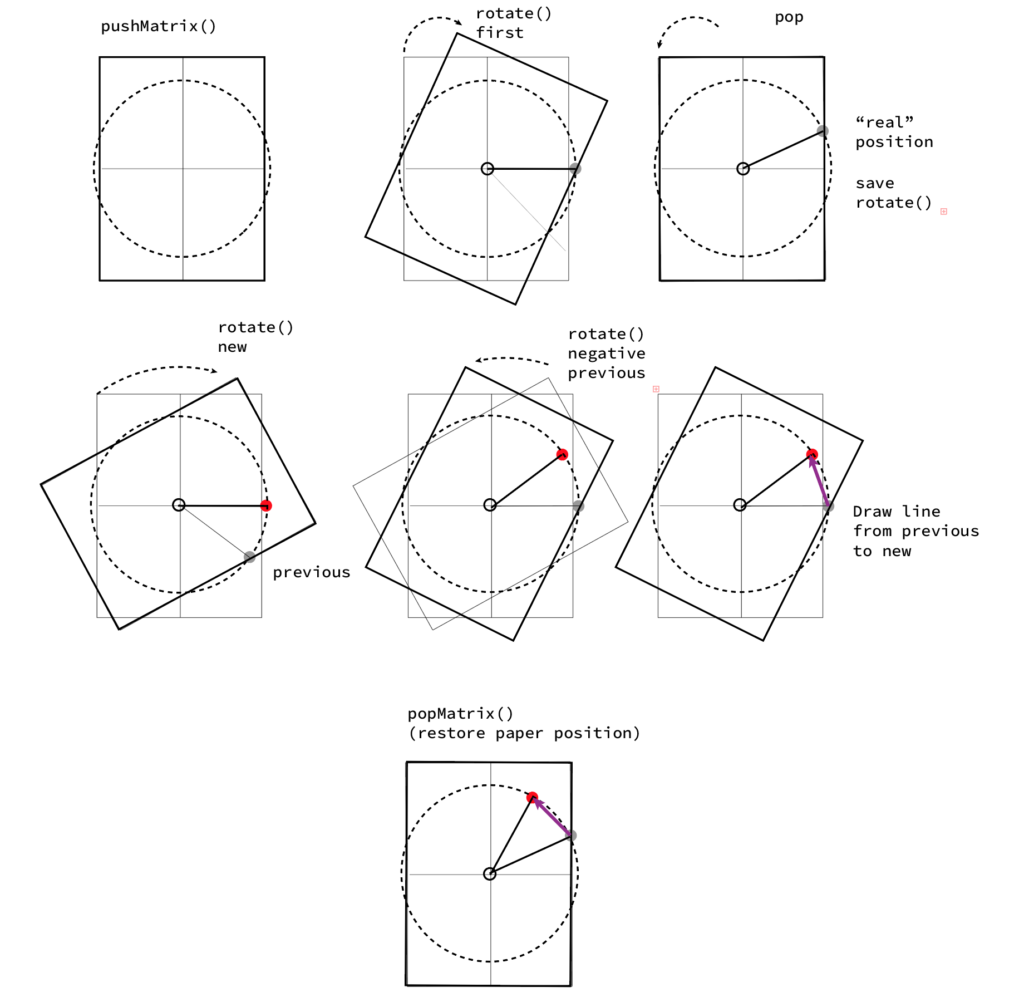
E sempre assim. Basta usar este código agora com um retrato e obtemos uma coisa… er… alguma coisa!… 😉
Sem mais demoras, aqui vai o resultado do algoritmo “Jorge-Nees”.

// PAmado, 2020-03-21 a partir da ideia de Maria Jorge / Georg Nees // declarar PImage retrato; // setup e inicialização size(2500, 2500); background(200, 0, 0); retrato = loadImage("leia.png"); int r = 25; retrato.resize(50, 50); noFill(); stroke(0); strokeWeight(4); // desenhar for ( int m = 0; m < retrato.width; m++) { for ( int n = 0; n < retrato.height; n++ ) { // desenhos dos circulos color c = retrato.get(m, n); int b = int( brightness(c) )/10; int loop = b; // 5 steps pushMatrix(); translate(m*r*2, n*r*2); for (int i = 0; i < loop; i++) { float pr = random(0, TWO_PI); rotate(pr); int px = int ( r*cos(-pr) ); int py = int ( r*sin(-pr) ); stroke(100, 0, 0); strokeWeight(1.5); line(px, py, r, 0); stroke(255); strokeWeight(2); point(r, 0); } popMatrix(); } }
Durante a tarde, voltamos à trigonometria. Quase que poderíamos ter resolvido o algoritmo anterior desta forma, e, também por isso, creio que merece fazer parte deste artigo.
A pergunta do Loudovico foi como obter uma “onda”, quase como aqueles padrões da calçada portuguesa.

Para perceber como se faz uma onda é preciso imaginar o movimento de um círculo, mas visto num “eixo horizontal de tempo”. Já calculámos a posição de um ponto no perímetro de um círculo no exemplo anterior. Por isso, fazendo um loop com todos os ângulos de uma circunferência conseguimos desenhar virtualmente todos os pontos de um circulo.
A explicação aparece mais ou menos aos 2h12m do vídeo da segunda sessão. Por isso, se quiserem acompanhar o live-coding, força nisso.
A ideia é usar as coordenadas (horizontais ou verticais como vamos usar neste exemplo) para descrever essa onda. Vamos começar com a representação da posição vertical de um ângulo (ai — pensam alguns—, que isto parece geometria!… — e querem saber? é mesmo! 😉
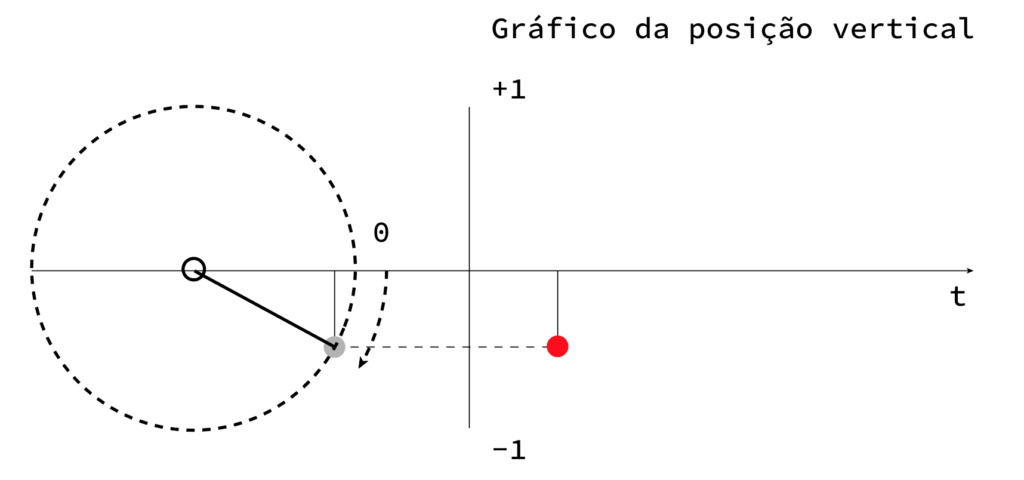
À medida que fazemos variar o ângulo da bola… isto é, à medida que a rodamos, se apenas representarmos a posição vertical, a bola parece que “oscila” para cima e para baixo.
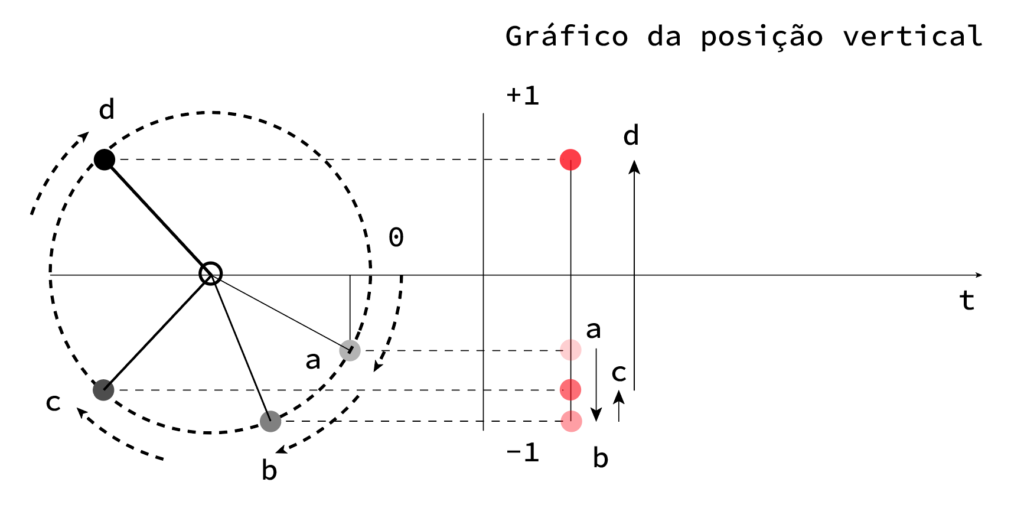
Basta então que “movamos” o ponto no tempo, isto é, usando o movimento vertical proporcionado pelo círculo, vamos desenhando a bola um pouco mais para a direita.
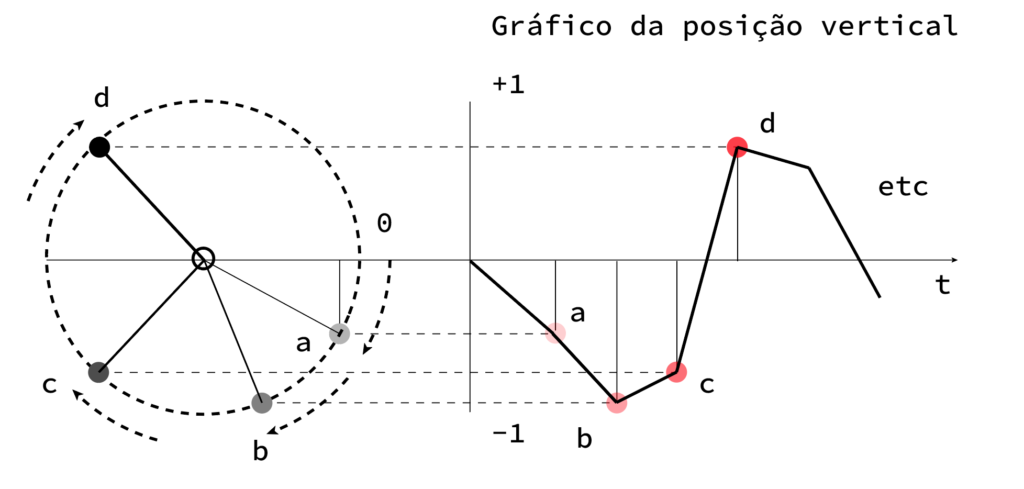
Et voilá… uma onda! Agora podemos juntar outra ligeiramente para a direita e para baixo e temos um exemplo pretendido. Ou, podemos fazer decair lentamente o raio (como a semana passada?) para fazer uma “cauda pesada”.
Aqui fica o exemplo. Basta aumentar o número de passos na rotação para ter uma onda mais ou menos fluida. Depende do desenho pretendido. Normalmente entre 32 a 64 passos dá bons resultados. Aqui estou a brincar com alguns mais, só pela piada.
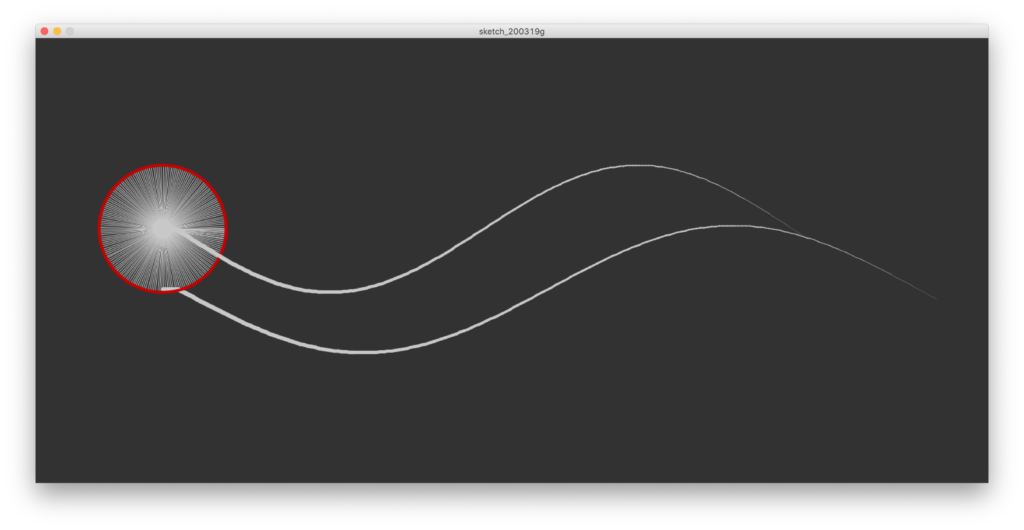
// PAmado, 2020-03-19 //Loudovico x Wavy lines explanation, Zoom LSI online seminar session // Declarar // Inicializar size(1500, 700); background(50); float raio = 100; float angulo = 0; smooth(); // try to get it a litle smoother on screen ;) noStroke(); translate(200, height/2-50); // adjust sketch position once ellipse(0, 0, 30, 30); // center // draw one line to the right to test noFill(); stroke(200); strokeWeight(1); line(0, 0, raio, 0); // when drawing, notice that we'll be drawing using trig functions sin and cos // calcular novo x e novo y com um angulo float nx, ny; nx = raio * cos(angulo); ny = raio * sin(angulo); noStroke(); fill(200, 0, 0); ellipse(nx, ny, 5, 5); // draw a new ball in the position calculated with angle // did it work?… cool! Now let's do a loop ;) int steps = 200; float px, py; // we will need these variables to store the previous position. It will alow us to create a "trail" effect. The wavvy line, remember? px = 0; py = 0; float px2 = 0; // do this if you want a second line… for (int i = 0; i < steps; i++) { angulo = i*TWO_PI/steps*1.03; // go slowly. multiply by an irregular factor to get it slighlty assymetrical nx = raio * cos(angulo); // calc the new angle every time ny = raio * sin(angulo); // get the circle going on noFill(); stroke(200); strokeWeight(1); line(0, 0, nx, ny); // draw to the new position noStroke(); fill(200, 0, 0); ellipse(nx, ny, 5, 5); // Now let's use the trail noFill(); stroke(200); // the line will get thinner as it strays away from the circle strokeWeight( 10 - map(i, 0, steps, 3, 10) ); // this is a really cool function that calculates "regra-de-três-simples". Basically it calculates the exchage between differnt scales of values. and it even allows to reverse map it // the x position of the line will step aways gradually nx = i*( (width/1.5) / steps ) +20; float nx2 = nx*1.2; line(px, py, nx, ny); line(px2, py+95, nx2, ny+95); noStroke(); fill(200, 0, 0); //ellipse(i*100+200, ny, 15, 15); px = nx; px2 = nx2; py = ny; }
