Second week of containment and isolation. Online classes continue to run with Colibri-Zoom. This one made with slightly higher assistance than last week (but not as popular as typography classes or type design!)
During the morning, he gave to (re)see some work in process. In a global way, all students seem to be understanding the objective, researching authors and performing interpretive graphic works from the estate / graphic style studied.

This time we just had a problem with one of the microphones during the session. Still text mode helped. Which was a little annoying, because the doubt that the student put – Ana Leite – was very cool and took a while to resolve.
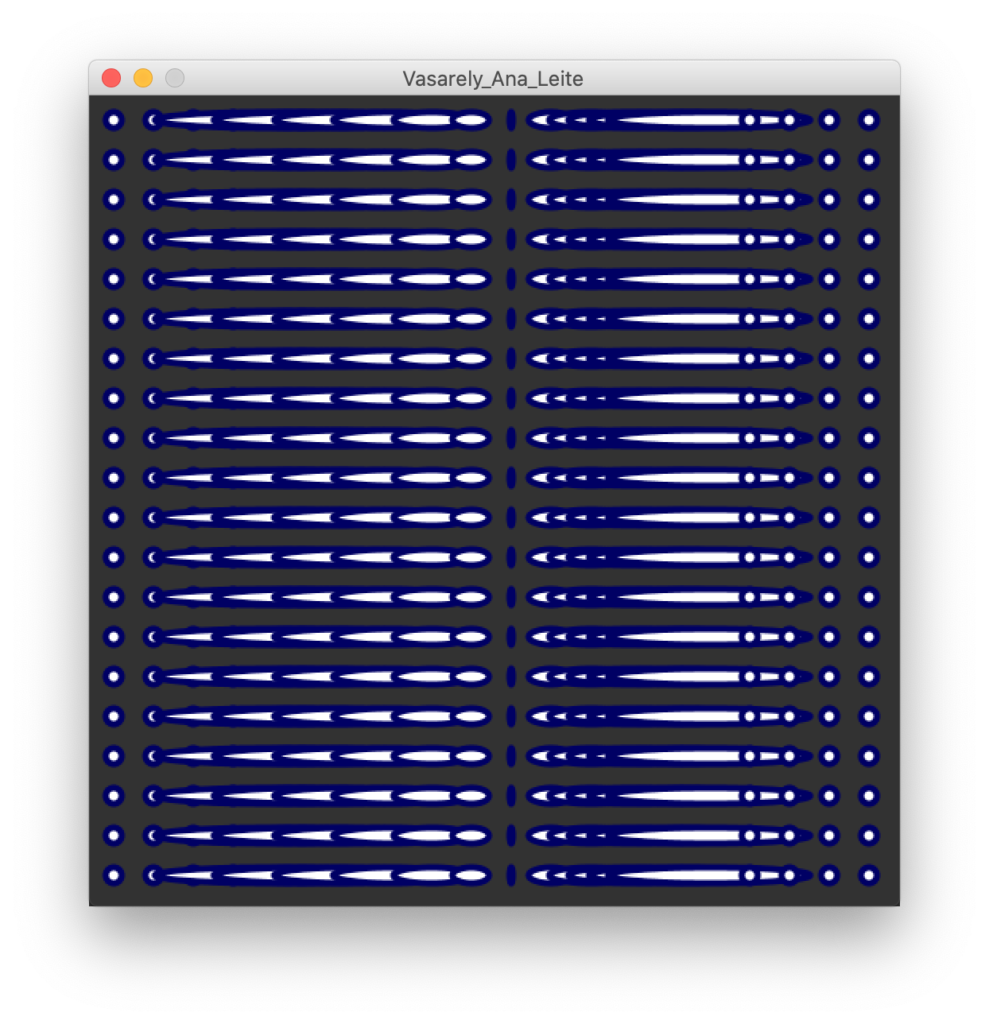
Her original work is a portrait of Victor Vasarely. The colors are still a bit psychedelic (I prefer by far the second), but the interesting thing to see was the displacement algorithm of the "pixels".

Victor Vasarely by Ana Leite

The most interesting and original aspect in these three years of Processing was to use color to make the spatial transformation of the pixel (first approach). Although it wasn't intentional, Ana is somehow using the color value to decide the height of the pixel. Almost like a depth map. Later I realized that she was looking for a kind of "lenticularization", a distortion of polar coordinates.

We still tried to adapt her code, but the time didn't go by much. I could do the basics, but I don't think the message went well. Her code was already very confusing (and the use of scale() was not allowing to see the changes in the best way).
This is a relatively simple algorithm to implement. That is, at this stage of the league, without complicating too much, only with ifs and without large complex variables (such as two-dimensional arrays that we will see for the week), it is possible to do with some effort of logic and visual commitment. Here's a quick try. First we start with a simple loop:

PAmado, 2020-03-21 From the interpretation of Ana Leite / Victor Vasarely declare variables ballsize int; int spacing; Sketch Setup size (510, 510); background(50); initialize variables ballSize = 20; spacing = 5; Draw translate(15, 15); move the page a bit to the left (to get the drawing more centered) do the loop with the shapes for (int i = 0; i< 20; i++) { for (int k = 0; k< 20; k++) { int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); stroke (0, 0, 100); strokeWeight(4); ellipse(x, y, ballSize, ballSize); } }
Then we move on to the algorithm. The idea of making a distortion of polar coordinates (pinch or zoom) is basically: the closer to the center (distortion) is each of these shapes, the more this distance affects its geometry. We have to remember that it's an inverted reason. That is, the shorter the distance, the greater the distortion.
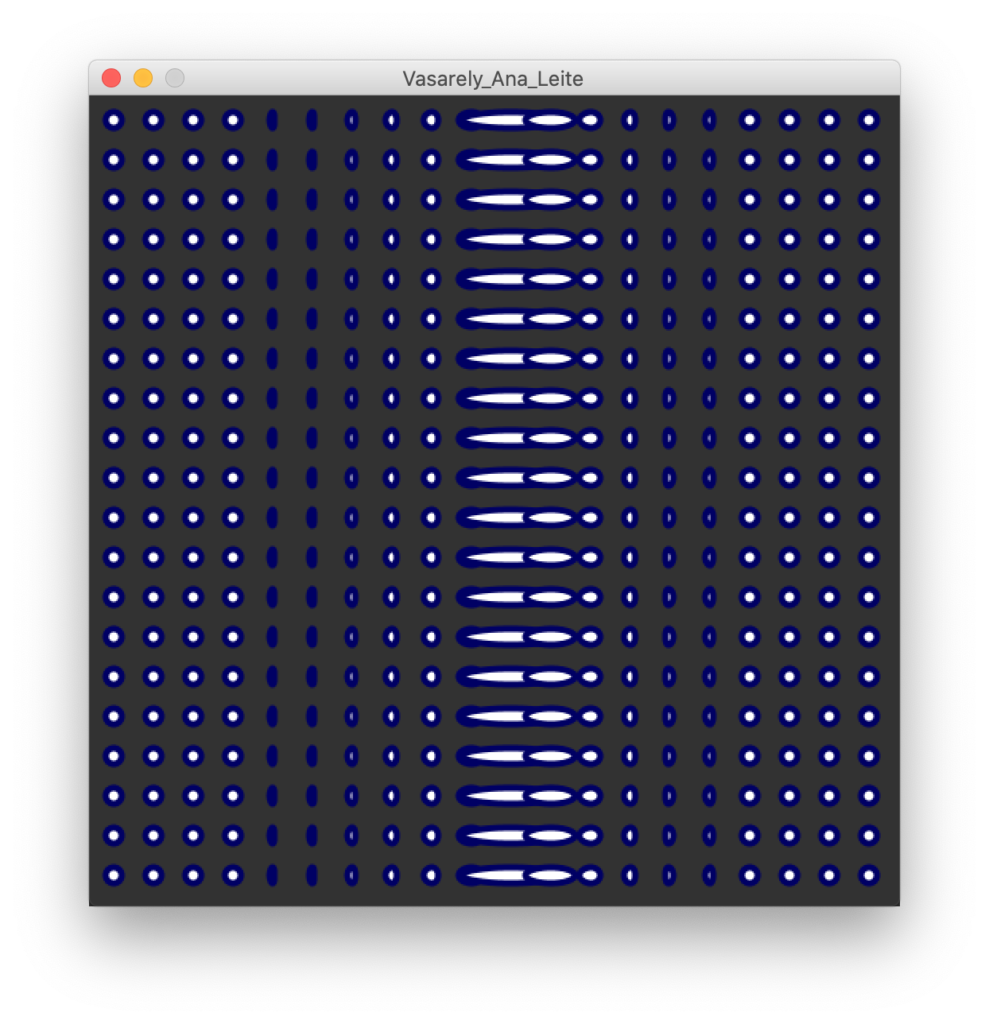
We move on to the example, only with the horizontal coordinates. In this sketch I needed to use some calculation operations. In particular the abs().
calculate the position int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); check if the position is within the distortion boundaries int dx = cx-x; check the distance (delta) between current x and the polar center int w = ballSize/2; calculate new dimensions If (ABS(DX)< boundaries ) { /* here we are using abs() to get the absolute (positive) number . You can also use dist() */ w = dx; }
In this example, the thing is strange, because we only use the distance to the center (if it is within the desired distortion radius) and use the distance value itself to distort. But if we use a map(), we can reverse the magnitude and immediately map to a more usable scale value/factor (I know this at this stage is able to be a little early/fast/complex, but in reality I've explained this to at least 3 students… the sooner the better?)
PAmado, 2020-03-21 From the interpretation of Ana Leite / Victor Vasarely declare variables ballsize int; int spacing; offset int; this will be used to center drawing on stage int cx, cy; this will be the center of the distortion target int boundaries; Sketch Setup size (510, 510); background(50); initialize variables ballSize = 20; spacing = 5; offset = 15; cx = width/2 - offset/2; cy = height/2 - offset/2; boundaries = 150; Draw translate (offset, offset); move the page a bit to the left (to get the drawing more centered) do the loop with the shapes for (int i = 0; i< 20; i++) { for (int k = 0; k< 20; k++) { calculate the position int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); check if the position is within the distortion boundaries int dx = cx-x; check the distance (delta) between current x and the polar center float w = ballSize/2; calculate new dimensions float fx = 1; If (ABS(DX)< boundaries ) { /* here we are using abs() to get the absolute (positive) number . You can also use dist() */ fx = map(dx, 0, boundaries*2, 0.2, 6); } stroke (0, 0, 100); strokeWeight(4); ellipse (x, y, w/fx, ballSize/2); always draw the ball with the size * scale factor. Don't' forget to invert the scaling: bigger as distance is shorter } }
And that's it. From here is to enjoy the colors and the shape of the pixels, using the horizontal and vertical coordinates.
The first approach gives freaks media results…
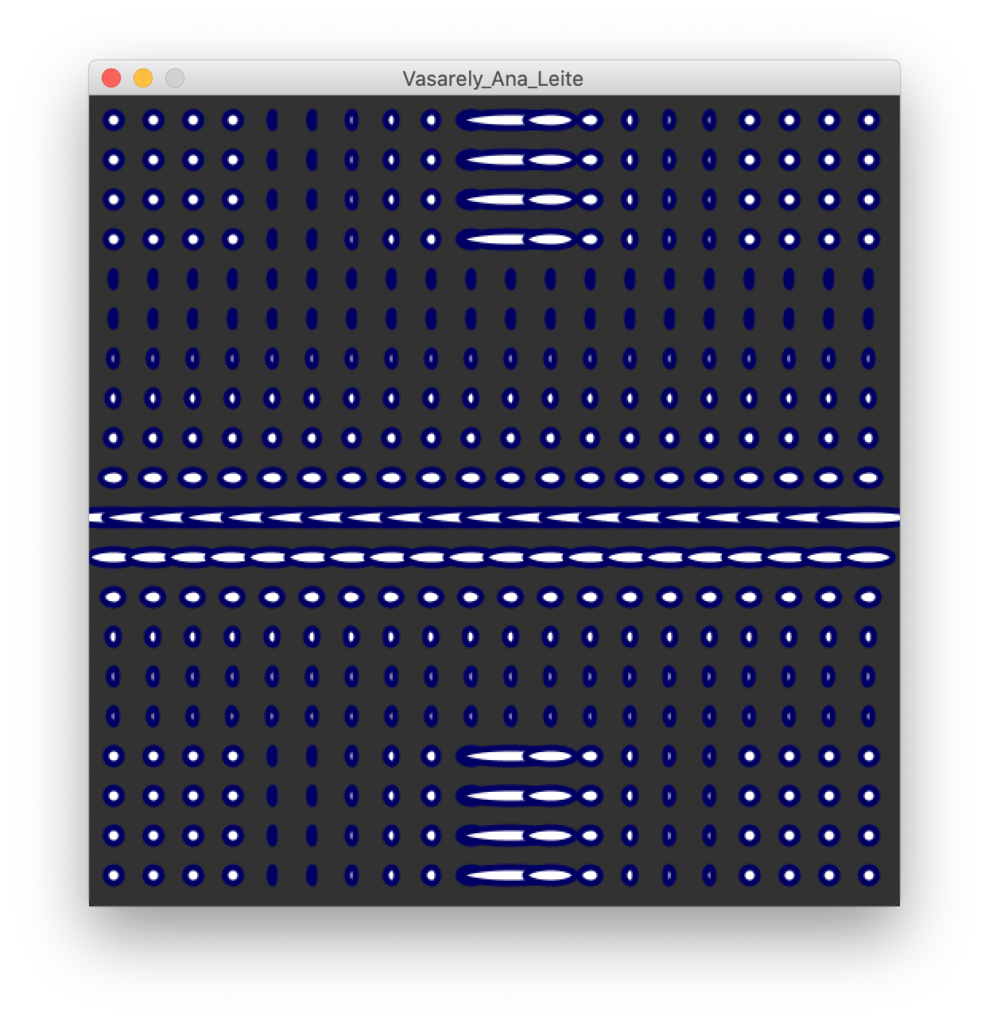
So it's time to try the dist()
float w = ballSize/2; calculate new dimensions float fx = 1; float fy = 1; if (dist(CX, CY, X, Y)< boundaries ) { /* changed into dist() instead of abs to calculate both*/ fx = map(dx, 0, boundaries, 0.5, 10); fy = map(dy, 0, boundaries, 0.5, 10); } stroke (0, 0, 100); strokeWeight(4); ellipse (x, y, w/fx, w/fy); always draw the ball with the size * scale factor. Don't' forget to invert the scaling: bigger as distance is shorter }
Et voila. It didn't look exactly the same, but it's already working. For a quick sketch it didn't look too bad. Now it's playing with the scale factor in a softer or progressive way and connecting this factor to a spatial lag.
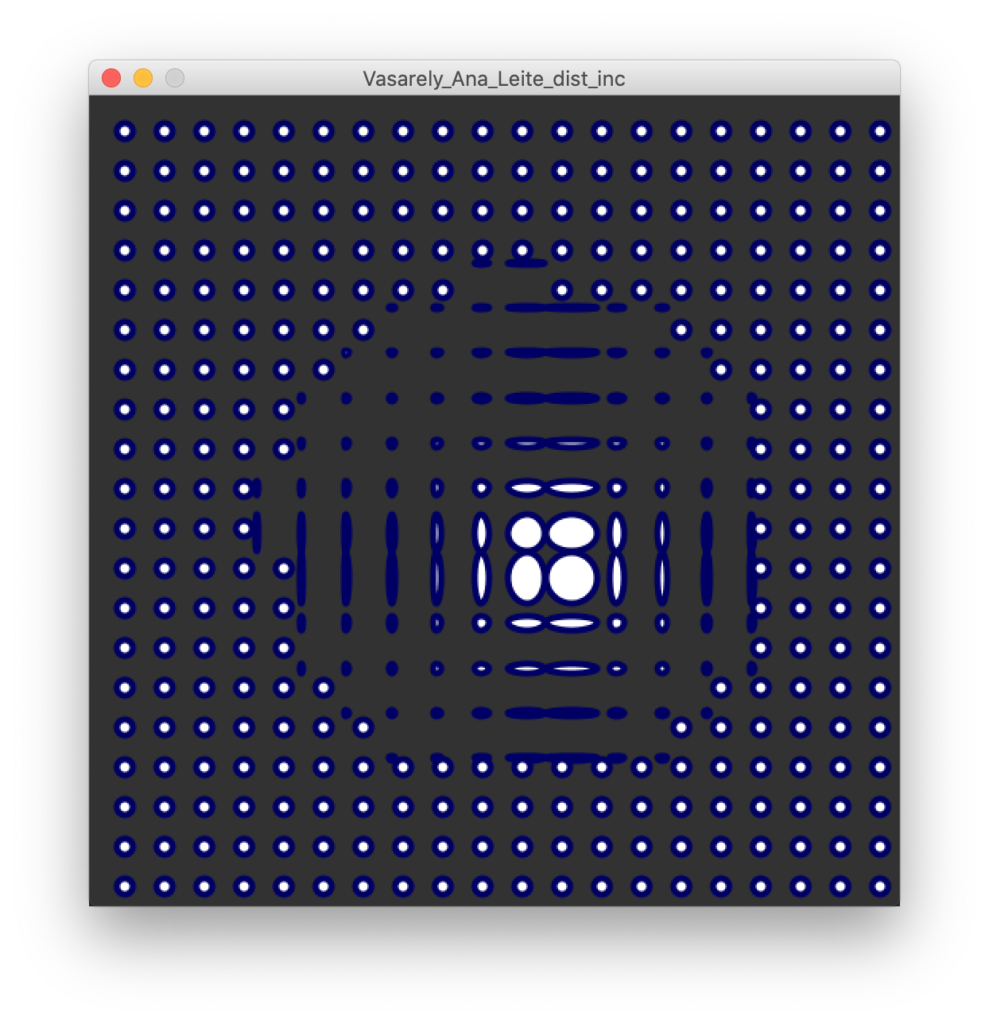
PAmado, 2020-03-21 From the interpretation of Ana Leite / Victor Vasarely declare variables ballsize int; int spacing; offset int; this will be used to center drawing on stage int cx, cy; this will be the center of the distortion target int boundaries; Sketch Setup size (510, 510); background(50); initialize variables ballSize = 20; spacing = 5; offset = 15; cx = width/2 - offset/2; cy = height/2 - offset/2; boundaries = 150; Draw translate (offset, offset); move the page a bit to the left (to get the drawing more centered) do the loop with the shapes for (int i = 0; i< 20; i++) { for (int k = 0; k< 20; k++) { calculate the position int x = k*(ballSize+spacing); int y = i*(ballSize+spacing); check if the position is within the distortion boundaries float dx = cx-x; check the distance (delta) between current x and the polar center float dy = cy-y; check the distance (delta) between current x and the polar center float w = ballSize/2; calculate new dimensions float fx = 1; float fy = 1; if (dist(CX, CY, X, Y)< boundaries ) { /* changed into dist() instead of abs to calculate both*/ fx = map(dx, 0, boundaries, 0.5, 5); fy = map(dy, 0, boundaries, 0.5, 5); } stroke (0, 0, 100); strokeWeight(4); float incx = map(fx, 0.5, 5, ballSize/2, -ballSize/2); float incy = map(fy, 0.5, 5, ballSize/2, -ballSize/2); ellipse (x + incx, y + incy, w/fx, w/fy); always draw the ball with the size * scale factor. Don't' forget to invert the scaling: bigger as distance is shorter } }
And good. In the next article I return to pushMatrix() transformations and trigonometry which was the most fun thing we were doing during the afternoon class (and that we will see in the next class).